题目内容
已知函数 且
且 ,在各项为正的数列{an}中,
,在各项为正的数列{an}中, 的前n项和为Sn,若Sn=126,则n= .
的前n项和为Sn,若Sn=126,则n= .
【答案】分析:由题意可得,f[f(- )]=2a-1可求a,进而可求f(x),由a1=2可得
)]=2a-1可求a,进而可求f(x),由a1=2可得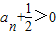 ,从而有
,从而有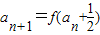 =2(
=2(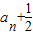 )-1=2an,利用等比数列的求和公式可求sn,结合已知可求n
)-1=2an,利用等比数列的求和公式可求sn,结合已知可求n
解答:解:由题意可得,f[f(- )]=f[
)]=f[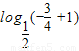 ]=f(2)=2a-1=3
]=f(2)=2a-1=3
∴a=2
∴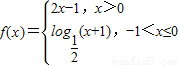
∵a1=2
∴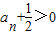
∴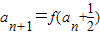 =2(
=2(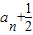 )-1=2an
)-1=2an
∴数列{an}是以2为首项,以2为公比的等比数列
∴Sn=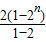 =2n+1-2=126
=2n+1-2=126
∴2n+1=128
∴n=6
故答案为6
点评:本题以函数的函数值的求解为载体,主要考查了利用数列的递推关系构造等比数列,进而求解数列的和,属于函数与数列知识的综合应用.
 )]=2a-1可求a,进而可求f(x),由a1=2可得
)]=2a-1可求a,进而可求f(x),由a1=2可得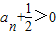 ,从而有
,从而有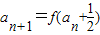 =2(
=2(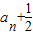 )-1=2an,利用等比数列的求和公式可求sn,结合已知可求n
)-1=2an,利用等比数列的求和公式可求sn,结合已知可求n解答:解:由题意可得,f[f(-
 )]=f[
)]=f[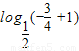 ]=f(2)=2a-1=3
]=f(2)=2a-1=3∴a=2
∴
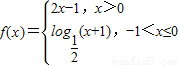
∵a1=2
∴
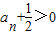
∴
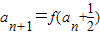 =2(
=2(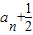 )-1=2an
)-1=2an∴数列{an}是以2为首项,以2为公比的等比数列
∴Sn=
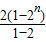 =2n+1-2=126
=2n+1-2=126∴2n+1=128
∴n=6
故答案为6
点评:本题以函数的函数值的求解为载体,主要考查了利用数列的递推关系构造等比数列,进而求解数列的和,属于函数与数列知识的综合应用.

练习册系列答案
相关题目
 且
且 ,在各项为正的数列
,在各项为正的数列 中,
中, 的前n项和为
的前n项和为 ,若
,若 = 。
= 。 且
且 ,在各项为正的数列{an}中,
,在各项为正的数列{an}中, 的前n项和为Sn,若Sn=126,则n= .
的前n项和为Sn,若Sn=126,则n= . 且
且 ,在各项为正的数列{an}中,
,在各项为正的数列{an}中, 的前n项和为Sn,若Sn=126,则n=( )
的前n项和为Sn,若Sn=126,则n=( ) 且
且