题目内容
（本题16分）已知椭圆C1：
上的点满足到两焦点的距离之和为4，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点。
(1) 求双曲线C2的方程；
(2) 若以椭圆的右顶点为圆心，该椭圆的焦距为半径作一个圆，一条过点P（1，1）直线与该圆相交，交点为A、B，求弦AB最小时直线AB的方程，求求此时弦AB的长。
解析：（1）由题意知m=2，则C1的方程为
………………3分
设双曲线C2的方程为
，则
故C2的方程为
………………8分
（2）圆方程为
，
根据圆的性质知：当
时，弦最小， ……………12分
所以
，得
，
所以直线AB的方程为
，即y=x。 ………………14分
圆心M到直线AB的距离为
，半径为
，
所以AB=
………………16分
练习册系列答案
优加精卷系列答案
相关题目
上的点满足到两焦点的距离之和为4，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点。
轴上,椭圆上的点到左、右焦点
的距离之和为
，离心率
.
（2）过左焦点
的直线
与椭圆C交于点
,以
为邻边作平行四边形
,求该平行四边形对角线
的长度的取值范围.
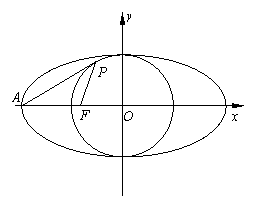（1）若P(－1，)，PA是⊙O的切线，求椭圆C的方程；
的右焦点为B（1，0），右准线与x轴的交点为A（5，0），过点A作直线
交椭圆C于两个不同的点P、Q．
，若存在，求出