题目内容
函数y=-x2-2x+3（-3≤x≤0）的值域是（ ）
| A、[0，3] |
| B、[0，4] |
| C、[3，4] |
| D、[-1，4] |
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：由条件利用二次函数的性质求得函数y=-x2-2x+3（-3≤x≤0）的值域．
解答：
解：∵函数y=-x2-2x+3=-（x+1）2+4 （-3≤x≤0），
故当x=-1时，函数取得最大值为4，当x=-3时，函数取得最小值为0，
故函数的值域为[0，4]，
故选：B．
故当x=-1时，函数取得最大值为4，当x=-3时，函数取得最小值为0，
故函数的值域为[0，4]，
故选：B．
点评：本题主要考查求二次函数在闭区间上的最值，二次函数的性质的应用，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（ ）
| A、若α⊥γ，β⊥γ，则α∥β |
| B、若m⊥α，n⊥α，则m∥n |
| C、若m∥α，n∥α，则m∥n |
| D、若m∥α，m∥β，则α∥β |
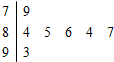如图是2012年元旦晚会举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的众数和中位数分别为（ ）| A、85，84 |
| B、84，84 |
| C、84，85 |
| D、85，85 |
下列函数中为奇函数的是（ ）
A、y=
| |||||||||
| B、y=2x | |||||||||
| C、y=x3 | |||||||||
D、y=lo
|