题目内容
已知椭圆 的焦点在
的焦点在 轴上,长轴长为
轴上,长轴长为 ,离心率为
,离心率为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点 和直线
和直线 :
: ,线段
,线段 是椭圆
是椭圆 的一条弦且直线
的一条弦且直线 垂直平
垂直平
分弦 ,求实数
,求实数 的值.
的值.
【答案】
(1)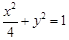 ;(2)
;(2)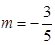 .
.
【解析】
试题分析:(1)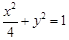 ;
;
(2)由条件可得直线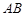 的方程为
的方程为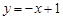 .于是,有
.于是,有
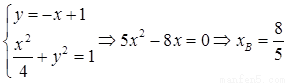 ,
,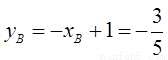 .
.
设弦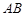 的中点为
的中点为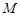 ,则由中点坐标公式得
,则由中点坐标公式得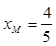 ,
,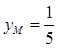 ,
,
由此及点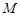 在直线
在直线 得
得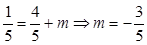 .
.
考点:本题主要考查椭圆标准方程,直线与椭圆的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆、标准方程时,主要运用了椭圆的几何性质。(II)小题中,运用中点坐标公式,得到直线l上的的坐标,代入假设方程,达到解题目的。

练习册系列答案
相关题目
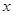 轴上,一个顶点为
轴上,一个顶点为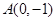 ,其右焦点到直线
,其右焦点到直线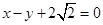 的距离为
的距离为 ,则椭圆的方程为 .
,则椭圆的方程为 .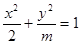 的焦点在
的焦点在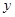 轴上,离心率为
轴上,离心率为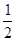 ,则
,则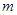 的值为( )
的值为( )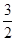 B.
B.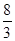 C.
C.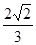 D.
D.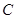 的焦点在
的焦点在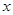 轴上,离心率
轴上,离心率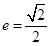 ,且经过点
,且经过点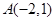 .
. 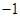 的直线
的直线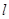 与椭圆
与椭圆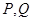 两点,求证:直线
两点,求证:直线 与
与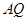 的倾斜角互补.
的倾斜角互补. 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率
的焦点,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线 ,交椭圆于A、B两点.
,交椭圆于A、B两点. ,求
,求 取值范围;
取值范围;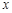 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线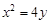 的焦点,离心率
的焦点,离心率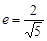 ,过椭圆的右焦点
,过椭圆的右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线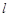 交椭圆于
交椭圆于 两点.
两点. 是线段
是线段 上的一个动点,且
上的一个动点,且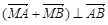 ,求
,求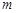 的取值范围;
的取值范围; 是点
是点 关于
关于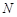 ,使得
,使得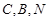 三点共线?若存在,求出定点
三点共线?若存在,求出定点