题目内容
已知椭圆的焦点在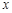 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线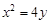 的焦点,离心率
的焦点,离心率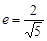 ,过椭圆的右焦点
,过椭圆的右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线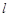 交椭圆于
交椭圆于 两点.
两点.
(1)求椭圆方程;
(2)设点 是线段
是线段 上的一个动点,且
上的一个动点,且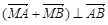 ,求
,求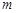 的取值范围;
的取值范围;
(3)设点 是点
是点 关于
关于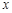 轴对称点,在
轴对称点,在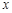 轴上是否存在一个定点
轴上是否存在一个定点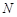 ,使得
,使得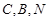 三点共线?若存在,求出定点
三点共线?若存在,求出定点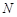 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】
(1)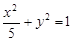
(2)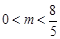
(3)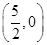
【解析】(1)由题意知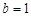 ,又
,又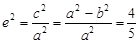 ,所以
,所以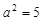 ,所以
,所以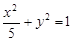 --------4分
--------4分
(2)由(1)得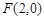 ,所以
,所以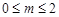 ,设
,设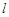 的方程为
的方程为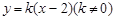 ,联立得
,联立得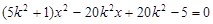 ,
,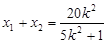 ,
,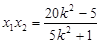 ,--------2分
,--------2分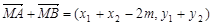 ,
,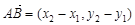 ,由题意得
,由题意得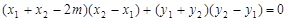 ,代入可得
,代入可得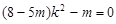 ,所以
,所以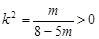 得
得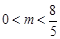 --------4分
--------4分
(3)设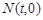 ,则有
,则有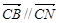 ,所以
,所以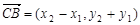 ,
,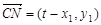 ,所以
,所以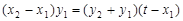 ,代入解得
,代入解得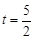 --------2分
--------2分

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
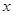 轴上,一个顶点为
轴上,一个顶点为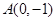 ,其右焦点到直线
,其右焦点到直线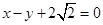 的距离为
的距离为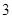 ,则椭圆的方程为 .
,则椭圆的方程为 .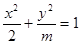 的焦点在
的焦点在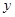 轴上,离心率为
轴上,离心率为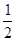 ,则
,则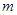 的值为( )
的值为( )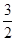 B.
B.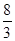 C.
C.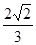 D.
D.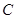 的焦点在
的焦点在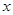 轴上,离心率
轴上,离心率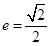 ,且经过点
,且经过点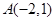 .
. 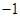 的直线
的直线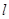 与椭圆
与椭圆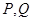 两点,求证:直线
两点,求证:直线 与
与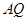 的倾斜角互补.
的倾斜角互补. 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率
的焦点,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线 ,交椭圆于A、B两点.
,交椭圆于A、B两点. ,求
,求 取值范围;
取值范围;