题目内容
【题目】如图所示圆锥中，
为底面圆的两条直径，
，且
，
，
为
的中点.求:
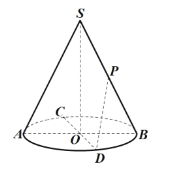
（1）该圆锥的表面积；
（2）异面直线
与
所成的角的大小（结果用反三角函数值表示）.
【答案】(1)
；(2) 
.
【解析】
(1)先计算出圆锥的母线长度，然后计算出圆锥的侧面积和底面积，即可计算出圆锥的表面积；
(2)连接
，根据位置关系可知异面直线
与
所成的角即为
或其补角，根据线段长度即可计算出
的值，即可求解出异面直线所成角的大小.
(1)因为
，所以
，
所以圆锥的侧面积为：
，圆锥的底面积为：
，
所以圆锥的表面积为：；
(2)连接，如下图所示：
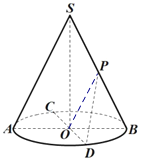
因为
为
的中点，
为
的中点，所以
且
，
所以异面直线与所成的角即为或其补角，
因为
，
，
，所以
平面
，
因为
平面，所以
，所以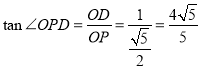
，
所以异面直线与所成的角的大小为：.
练习册系列答案
阅读快车系列答案
相关题目
