题目内容
下列说法中,其中正确命题的序号为
①x>2是x2-3x+2>0的充分不必要条件.
②函数y=
图象的对称中心是(1,1).
③若函数f(x)=
,对任意的x1≠x2都有
<0,则实数a的取值范围是(
,1).
①
①
.:①x>2是x2-3x+2>0的充分不必要条件.
②函数y=
| x-1 |
| x+1 |
③若函数f(x)=
|
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 7 |
分析:①根据充分条件和必要条件的定义进行判断.②根据分式函数的性质判断.③根据分段函数的单调性进行判断.
解答:解:①由x2-3x+2>0得x>2或x<1,即x>2是x2-3x+2>0的充分不必要条件,∴①正确.
②由y=
得y=
=1-
,则根据分式函数性质可知函数关于(-1,1)对称,∴②错误.
③若对任意的x1≠x2都有
<0,则函数满足f(x)为减函数,则有
,即
,解得
≤a<
,∴③错误.
∴正确的命题为①.
故答案为:①
②由y=
| x-1 |
| x+1 |
| x+1-2 |
| x+1 |
| 2 |
| x+1 |
③若对任意的x1≠x2都有
| f(x2)-f(x1) |
| x2-x1 |
|
|
| 1 |
| 7 |
| 1 |
| 3 |
∴正确的命题为①.
故答案为:①
点评:本题主要考查充分条件和必要条件的应用,以及分式函数的性质,以及分段函数的单调性的应用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
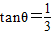 ,则
,则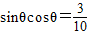 .
.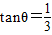 ,则
,则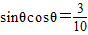 .
.