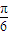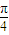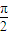题目内容
己知双曲线C的方程为 ,若直线x-my-3=0截双曲线的一支所得弦长为5.
,若直线x-my-3=0截双曲线的一支所得弦长为5.(Ⅰ)求m的值;
(Ⅱ)设过双曲线C上的一点P的直线与双曲线的两条渐近线分别交于点P1、P2,且点P分有向线段
 所成的比为λ(λ>0),当
所成的比为λ(λ>0),当 时,求
时,求 (O为坐标原点)的值.
(O为坐标原点)的值.
【答案】分析:(Ⅰ)由曲线C的方程为 ,得
,得 ,c=2,e=
,c=2,e= ,左、右焦点分别为:F1(-3,0),F2(3,0),故直线x-my-3=0恒过双曲线的右焦点F2(3,0),于是直线与双曲线的右支相交,由双曲线的第二定义得:
,左、右焦点分别为:F1(-3,0),F2(3,0),故直线x-my-3=0恒过双曲线的右焦点F2(3,0),于是直线与双曲线的右支相交,由双曲线的第二定义得: =e,由此能求出m.
=e,由此能求出m.
(Ⅱ)双曲线C的两条渐近线方程分别为 ,
, ,设P(x,y),P1(x1,y1),P2(x2,y2),且点P分有向线段
,设P(x,y),P1(x1,y1),P2(x2,y2),且点P分有向线段 所成的比为λ(λ>0),则
所成的比为λ(λ>0),则 ,
, ,
, ,由此能求出
,由此能求出 (O为坐标原点)的值.
(O为坐标原点)的值.
解答:解:(Ⅰ)由曲线C的方程为 ,
,
得 ,∴c=2,e=
,∴c=2,e= ,
,
左、右焦点分别为:F1(-3,0),F2(3,0),
∴直线x-my-3=0恒过双曲线的右焦点F2(3,0),
于是直线与双曲线的右支相交,
设两个交点坐标分别为A(x1,y1)、B(x2,y2),
由双曲线的第二定义得: =e,
=e,
即|AF2|= .
.
同理, ,
,
∴|AB|=|AF2|+|BF2|= ,
,
依题意,得 ,
,
∴x1+x2=6,
由直线过右焦点F2(3,0),知x1=x2=3,
此时直线垂直于x轴,
∴m=0.
(Ⅱ)双曲线C的两条渐近线方程分别为 ,
, ,
,
设P(x,y),P1(x1,y1),P2(x2,y2),且点P分有向线段 所成的比为λ(λ>0),
所成的比为λ(λ>0),
则 ,
, ,
, ,
,
∵点P(x,y)在双曲线 上,
上,
∴ ,
,
化简,得 ,
,
∵ =
= ,
,
同理,得 ,
,
∴ ,(λ>0),
,(λ>0),
当 时,
时, =
= .
.
点评:本题考查双曲线与直线的位置关系的综合应用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
 ,得
,得 ,c=2,e=
,c=2,e= ,左、右焦点分别为:F1(-3,0),F2(3,0),故直线x-my-3=0恒过双曲线的右焦点F2(3,0),于是直线与双曲线的右支相交,由双曲线的第二定义得:
,左、右焦点分别为:F1(-3,0),F2(3,0),故直线x-my-3=0恒过双曲线的右焦点F2(3,0),于是直线与双曲线的右支相交,由双曲线的第二定义得: =e,由此能求出m.
=e,由此能求出m.(Ⅱ)双曲线C的两条渐近线方程分别为
 ,
, ,设P(x,y),P1(x1,y1),P2(x2,y2),且点P分有向线段
,设P(x,y),P1(x1,y1),P2(x2,y2),且点P分有向线段 所成的比为λ(λ>0),则
所成的比为λ(λ>0),则 ,
, ,
, ,由此能求出
,由此能求出 (O为坐标原点)的值.
(O为坐标原点)的值.解答:解:(Ⅰ)由曲线C的方程为
 ,
,得
 ,∴c=2,e=
,∴c=2,e= ,
,左、右焦点分别为:F1(-3,0),F2(3,0),
∴直线x-my-3=0恒过双曲线的右焦点F2(3,0),
于是直线与双曲线的右支相交,
设两个交点坐标分别为A(x1,y1)、B(x2,y2),
由双曲线的第二定义得:
 =e,
=e,即|AF2|=
 .
.同理,
 ,
,∴|AB|=|AF2|+|BF2|=
 ,
,依题意,得
 ,
,∴x1+x2=6,
由直线过右焦点F2(3,0),知x1=x2=3,
此时直线垂直于x轴,
∴m=0.
(Ⅱ)双曲线C的两条渐近线方程分别为
 ,
, ,
,设P(x,y),P1(x1,y1),P2(x2,y2),且点P分有向线段
 所成的比为λ(λ>0),
所成的比为λ(λ>0),则
 ,
, ,
, ,
,∵点P(x,y)在双曲线
 上,
上,∴
 ,
,化简,得
 ,
,∵
 =
= ,
,同理,得
 ,
,∴
 ,(λ>0),
,(λ>0),当
 时,
时, =
= .
.点评:本题考查双曲线与直线的位置关系的综合应用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
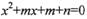 的两根分别为椭圆和双曲线的离心率.记分别以m、n为横纵坐标的点P(m,n)表示的平面区域为D,若函数
的两根分别为椭圆和双曲线的离心率.记分别以m、n为横纵坐标的点P(m,n)表示的平面区域为D,若函数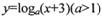 的图象上存在区域D上的点,则实数a的取值范围为
的图象上存在区域D上的点,则实数a的取值范围为 B、
B、 C、
C、 D、
D、
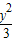 =1,直线m的方程为x=
=1,直线m的方程为x= ,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧
,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧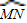 的长度为n,则
的长度为n,则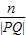 的值为( )
的值为( )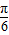
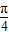
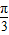
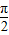
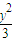 =1,直线m的方程为x=
=1,直线m的方程为x= ,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧
,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧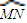 的长度为n,则
的长度为n,则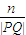 的值为( )
的值为( )