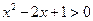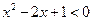题目内容
若空间中有四个点,则“这四个点中没有三点在同一直线上”是“这四个点不在
同一平面上”的 ( )
同一平面上”的 ( )
| A.充分非必要条件; | B.必要非充分条件; | C.充要条件; | D.非充分非必要条件; |
B
考点:
分析:由题意知,用由一条直线和直线外一点确定一个平面验证充分性成立,反之必要性不成立.
解答:解:充分性成立:“这四个点中有三点在同一直线上”,则第四点不在共线三点所在的直线上,
由一条直线和直线外一点确定一个平面,推出“这四点在唯一的一个平面内”;
必要性不成立:“四个点在同一平面上”可能推出“两点分别在两条相交或平行直线上”;
故答案为:充分非必要.
点评:本题考查了确定平面的依据:即公理2和推论,还有必要条件、充分条件与充要条件的判断
分析:由题意知,用由一条直线和直线外一点确定一个平面验证充分性成立,反之必要性不成立.
解答:解:充分性成立:“这四个点中有三点在同一直线上”,则第四点不在共线三点所在的直线上,
由一条直线和直线外一点确定一个平面,推出“这四点在唯一的一个平面内”;
必要性不成立:“四个点在同一平面上”可能推出“两点分别在两条相交或平行直线上”;
故答案为:充分非必要.
点评:本题考查了确定平面的依据:即公理2和推论,还有必要条件、充分条件与充要条件的判断

练习册系列答案
相关题目
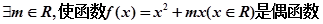 。
。 。
。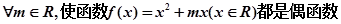 。
。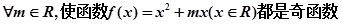 。
。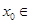 R,
R,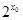
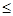 0”的否定是( ).
0”的否定是( ). 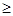 0
0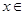 R,
R, 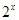
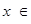 R,
R, 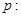
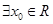 ,
,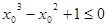 , 则
, 则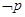 是_____________________;
是_____________________;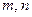 为空间的两条直线,
为空间的两条直线,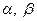 为空间的两个平面,给出下列命题:
为空间的两个平面,给出下列命题: 1)若
1)若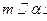 ,
,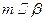 , 则
, 则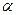 ∥
∥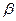 ; (2)若
; (2)若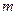 ⊥
⊥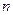 ∥
∥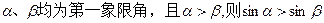

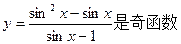 ④函数
④函数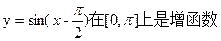
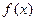 满足
满足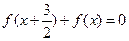 且函数
且函数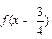 为奇函数,给
为奇函数,给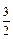 ,(2))函数
,(2))函数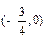 对称,(3)
对称,(3)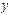 对称,则其中正确的命题序
对称,则其中正确的命题序 号是
号是
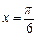 ”是“
”是“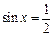 ”的充分不必要条件;
”的充分不必要条件; 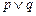 ”为真,则“
”为真,则“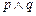 ”为真;
”为真;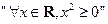 的否定是
的否定是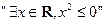 ;
;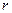 的绝对值越接近于
的绝对值越接近于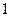 ,表明两个随机变量线性相关性越强;
,表明两个随机变量线性相关性越强;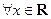 ,
,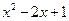 ≥0”的否定是 ( )
≥0”的否定是 ( )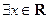 ,
,