题目内容
已知双曲线的方程为
-
=1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为
c(c为双曲线的半焦距长),则双曲线的离心率为
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
分析:根据双曲线方程可得它的渐近线方程为bx±ay=0,焦点坐标为(±c,0).利用点到直线的距离,结合已知条件列式,可得b=
c,再用平方关系可算出a=
c,最后利用双曲线离心率的公式,可以计算出该双曲线的离心率.
| ||
| 3 |
| 2 |
| 3 |
解答:解:双曲线
-
=1的渐近线方程为bx±ay=0,焦点坐标为(±c,0),其中c=
∴一个焦点到一条渐近线的距离为d=
=
c,即b=
c,
因此,a=
=
c,由此可得双曲线的离心率为e=
=
故答案为:
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
∴一个焦点到一条渐近线的距离为d=
| |±bc| | ||
|
| ||
| 3 |
| ||
| 3 |
因此,a=
| c2-b2 |
| 2 |
| 3 |
| c |
| a |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题给出双曲线一个焦点到渐近线的距离与焦距的关系,求双曲线的离心率,着重考查了双曲线的标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
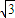 y=0和x+
y=0和x+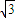 y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )
y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )