题目内容

已知Sn=1+
3
2
+
5
22
+…+
2n-1
2n-1
，则Sn等于（　　）
A、5-
n+2
2n-2
B、4-
2n+1
2n-1
C、3-
2n-1
2n-1
D、6-
2n+3
2n-1
考点：数列的求和
专题：等差数列与等比数列
分析：根据题意选择错位相减法求出Sn．
解答： 解：由题意得，Sn=1+
3
2
+
5
22
+…+
2n-1
2n-1
，①
则
1
2
Sn=
1
2
+
3
22
+
5
23
+…+
2n-1
2n
，②
①-②得，
1
2
Sn=1+2（
1
2
+
1
22
+…+
1
2n-1
）-
2n-1
2n

=1+2×
1
2
(1-
1
2n-1
)
1-
1
2
-
2n-1
2n
=3-
2n+3
2n

所以Sn=6-
2n+3
2n-1
，
故选：D．
点评：本题考查了错位相减法求数列的和，这是常考的求和方法，根据通项公式的特点选择恰当的求和方法．
练习册系列答案
相关题目
与双曲线x2-
y2
4
=1有共同的渐近线，且过点（2，2）的双曲线方程为（　　）
A、
y2
3
-
x2
12
=1
B、
y2
2
-
x2
8
=1
C、
x2
2
-
y2
8
=1
D、
x2
3
-
y2
12
=1
已知函数f（x）=ax3+bx2+cx在x0处取得极小值-2，使其导函数f′（x）＜0的范围为（-1，1）
（Ⅰ）求x0的值及f（x）的解析式
（Ⅱ） 设点A为函数f（x）图象上极大值对应的点，曲线f（x）在点A处的切线l1交f（x）的图象于另一点B，且曲线f（x）在点B处的切线l2，在原点O处的切线为l，直线l1，l2分别与直线l交于M，N，求证：
NO
=2
OM
．
若P点在△ABC确定的平面上，O为平面外一点，下列说法中不正确的是（　　）
A、
OA
、
OB
、
OC
是共面向量
B、若
OP
=x
OA
+y
OB
，则P点在面OAB上
C、
AP
、
AB
、
AC
是共面向量
D、若P点是△ABC的重心，则
OP
=
1
3
OA
+
1
3
OB
+
1
3
OC
已知
AB
=(2，2，1)，
CD
=(4，5，3)，则平面ABC的单位法向量是
 
．
在黄兴路步行街同侧有8块广告牌，牌的底色可选用红、蓝两种颜色，若只要求相邻两块牌的底色不都为红色，则不同的配色方案共有
 
种．
已知数列{an}的前n项的和Sn=（n+1）bn，其中{bn}是首项为1，公差为2的等差数列．
（1）求数列{an}的通项公式；
（2）若cn=
1
an(2bn+5)
，求数列{cn}的前n项和Tn．
关于x的不等式lg（20-5x2）＞lg（a-x）+1的整数解只有1，则实数a的取值范围是
 
．
如下图①对应于函数f（x），则在下列给出的四个函数中，图②对应的函数只能是（　　）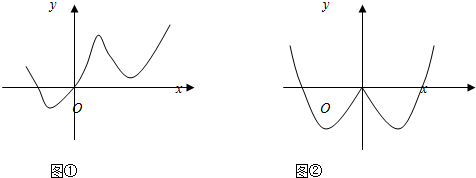
A、y=f（|x|）
B、y=|f（x）|
C、y=f（-|x|）
D、y=-f（|x|）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网