题目内容
有甲、乙、丙、丁四名深圳大运会志愿者被随机地分到A,B,C三个不同的岗位服务,若A岗位需要两名志愿者,B,C岗位各需要一名志愿者。甲、乙两人同时不参加A岗位服务的概率是 ;甲不在A岗位,乙不在B岗位,丙不在C岗位,这样安排服务的概率是 。
 ,
,
解析试题分析:设对不同志愿者的安排按顺序对应三个不同的岗位,则岗位A需要两名志愿者,岗位B.C各需要一名志愿者的所有可能的结果为:(甲乙、丙、丁),(甲乙、丁、丙), (甲丙、乙、丁),(甲丙、丁、乙), (甲丁、乙、丙), (甲丁、丙、乙), (乙丙、甲、丁),(乙丙、丁、甲), (乙丁、甲、丙), (乙丁、丙、甲), (丙丁、甲、乙), (丙丁、乙、甲), 共有12种不同的情况,每种基本事件的可能性相同,是古典概型的概率问题,所以
设甲、乙两人同时不参加A岗位服务的事件为M,则它的对立事件,即甲、乙同在A岗位有 (甲乙、丙、丁),(甲乙、丁、丙),共2种不同情况,所以概率为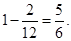 其中甲不在A岗位,乙不在B岗位,丙不在C岗位的情况有4种,所以概率为
其中甲不在A岗位,乙不在B岗位,丙不在C岗位的情况有4种,所以概率为
考点:本小题主要考查古典概型概率的求解.
点评:求解古典概型概率时,要保证每个基本实际都是等可能的.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为 ,则展开式中常数项是______.
,则展开式中常数项是______. 展开式中二项式系数之和是1024,常数项为
展开式中二项式系数之和是1024,常数项为 ,则实数
,则实数 的值是
的值是  的展开式中
的展开式中 的系数等于
的系数等于 的系数的4倍,则n等于 .
的系数的4倍,则n等于 . 的展开式中常数项的系数为_____________.
的展开式中常数项的系数为_____________.