题目内容
若三点A(2,-3)、B(4,3)、C(5,k)在同一条直线上,请求出k的取值.
由直线上两点的斜率公式得
kAB= ,kBC=k-3.
,kBC=k-3.
故k-3=3,解得k=6.
kAB=
 ,kBC=k-3.
,kBC=k-3.故k-3=3,解得k=6.
若A、B、C均在斜率k存在的直线l上,那么任意两点的坐标都可表示直线l的斜率k,即kAB=kAC=kBC;反过来,若kAB=kAC,则AB的倾斜角与AC的倾斜角相同,AB与AC所在直线重合.利用它们可证明诸点共线或与此有关的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的倾斜角是 .
的倾斜角是 . ,且过点A(1,5)的直线l与x轴交于点P,则点P的坐标为( )
,且过点A(1,5)的直线l与x轴交于点P,则点P的坐标为( ) 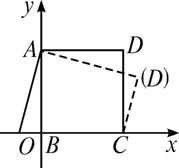
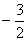
 及点
及点 的直线的倾斜角介于
的直线的倾斜角介于 与
与 之间,求
之间,求 的范围.
的范围. 为何值时,经过两点
为何值时,经过两点 (-
(- (1,
(1, )的直线的斜率是12.
)的直线的斜率是12. 的倾斜角为
的倾斜角为



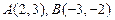 ,若直线
,若直线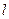 过点
过点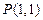 与线段
与线段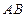 相交,则直线
相交,则直线 的取值范围是( ).
的取值范围是( ).


