题目内容
已知函数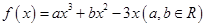 在点
在点 处的切线方程为
处的切线方程为 .
.
⑴求函数 的解析式;
的解析式;
⑵若对于区间 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数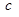 的最小值;
的最小值;
⑶若过点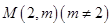 可作曲线
可作曲线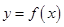 的三条切线,求实数
的三条切线,求实数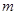 的取值范围.
的取值范围.
(1)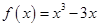 ;(2)4;(3)
;(2)4;(3)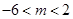 .
.
解析试题分析:(1)利用切点处的切线的斜率就是切点处的导数可列关于 一个的等式,再根据切点既在曲线上又在切线上又可列出关于
一个的等式,再根据切点既在曲线上又在切线上又可列出关于 一个的等式,联立即可解出关于
一个的等式,联立即可解出关于 ,从而求出函数
,从而求出函数 (2)对于区间
(2)对于区间 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,可转化为
,可转化为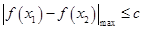 ,再转化为
,再转化为 ,而
,而 利用导数判断单调性后易求;(3)可设切点为
利用导数判断单调性后易求;(3)可设切点为 ,求出切线方程后,将
,求出切线方程后,将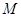 点坐标代入可得关于
点坐标代入可得关于 的三次方程,过点
的三次方程,过点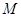 可作曲线
可作曲线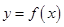 的三条切线,则表示这个方程有三个不同的解,再转化为三次函数的零点的判断,可求极值用数形结合的方法解决,这是我们所熟悉的问题.
的三条切线,则表示这个方程有三个不同的解,再转化为三次函数的零点的判断,可求极值用数形结合的方法解决,这是我们所熟悉的问题.
试题解析:⑴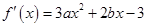 . 2分
. 2分
根据题意,得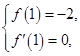 即
即 解得
解得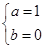 3分
3分
所以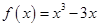 . 4分
. 4分
⑵令 ,即
,即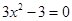 .得
.得 .
.

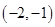
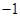
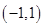
1 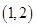
2 
+ 
+ 

 练习册系列答案
练习册系列答案
优佳百分卷系列答案
秒杀小题系列答案
顶尖卷王系列答案
小卷实战系列答案

本土教辅名校学案初中生辅导系列答案
轻巧夺冠青岛专用系列答案
名题文化步步高书系名题系列答案
倍速训练法一练通系列答案
金牌教辅夺冠金卷系列答案
相关题目
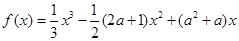 .
.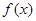 在
在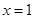 处取得极大值,求实数
处取得极大值,求实数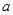 的值;
的值;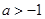 ,求
,求 上的最大值.
上的最大值.
 在
在 上是增函数,
上是增函数, 的取值集合
的取值集合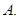 ;
;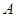 中的最小值时,定义数列
中的最小值时,定义数列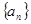 ;满足
;满足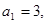 且
且 ,
,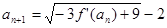 ,求数列
,求数列 ,数列
,数列 的前
的前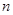 项和为
项和为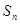 ,求证:
,求证: .
.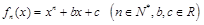
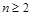 ,
,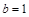 ,
,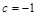 ,证明:
,证明: 在区间
在区间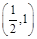 内存在唯一的零点;
内存在唯一的零点;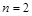 ,若对任意
,若对任意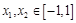 ,均有
,均有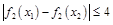 ,求
,求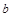 的取值范围.
的取值范围.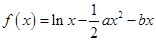 .
.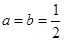 时,求函数
时,求函数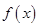 的最大值;
的最大值;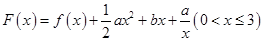 其图象上任意一点
其图象上任意一点 处切线的斜率
处切线的斜率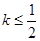 恒成立,求实数
恒成立,求实数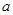 的取值范围;
的取值范围; ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. 若函数
若函数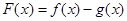 在x = 0处取得极值.
在x = 0处取得极值.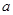 的值;
的值; 在区间[0,2]上恰有两个不同的实数根,求实数
在区间[0,2]上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; 都成立.
都成立.
 时,若存在
时,若存在 使得对任意的
使得对任意的 恒成立,求
恒成立,求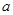 的取值范围。
的取值范围。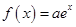 ,
,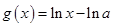 ,其中
,其中 为常数,
为常数, ,函数
,函数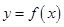 和
和 的图像在它们与坐标轴交点处的切线分别为
的图像在它们与坐标轴交点处的切线分别为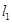 、
、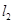 ,且
,且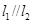 .
. 和
和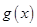 公共定义域内的任意实数
公共定义域内的任意实数 ,有
,有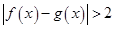 ;
;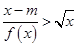 成立,求实数
成立,求实数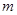 的取值范围.
的取值范围.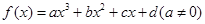
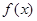 的图象关于原点对称,当
的图象关于原点对称,当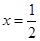 时,
时,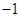 ,求
,求 的解析式。
的解析式。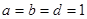 ,
, 上的单调函数,求
上的单调函数,求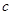 的取值范围
的取值范围