题目内容

已知△ABC中，cotA=-
12
5
，则cosA=（　　）
A、
12
13
B、
5
13
C、-
5
13
D、-
12
13
分析：利用同角三角函数的基本关系cosA转化成正弦和余弦，求得sinA和cosA的关系式，进而与sin2A+cos2A=1联立方程求得cosA的值．
解答：解：∵cotA=-
12
5

∴A为钝角，cosA＜0排除A和B，
再由cotA=
cosA
sinA
=-
12
5
，和sin2A+cos2A=1求得cosA=-
12
13
，
故选D．
点评：本题考查同角三角函数基本关系的运用．主要是利用了同角三角函数中的平方关系和商数关系．
练习册系列答案
相关题目
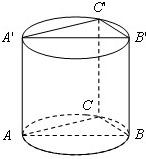精英家教网如图，直三棱柱ABC-A′B′C′内接于高为
2
的圆柱中，已知∠ACB=90°，AA′=
2
，BC=AC=1，O为AB的中点．
求（1）圆柱的全面积；
（2）异面直线AB′与CO所成的角的大小；
（3）求二面角A′-BC-A的大小．
精英家教网已知O是△ABC内任意一点，连接AO，BO，CO并延长交对边于A′，B′，C′，则
OA/
AA/
+
OB/
BB/
+
OC/
CC/
=1，这是平面几何中的一个命题，其证明方法常采用“面积法”：
OA/
AA/
+
OB/
BB/
+
OC/
CC/
=
S△OBC
S△ABC
+
S△OCA
S△ABC
+
S△OAB
S△ABC
=
S△ABC
S△ABC
=1．运用类比猜想，对于空间四面体存在什么类似的命题？并用“体积法”证明．
已知O是△ABC内任意一点，连结AO，BO，CO并延长交对边于A′，B′，C′，则
OA′
AA′
+
OB′
BB′
+
OC′
CC′
=1，这是平面几何中的一个命题，运用类比猜想，对于空间四面体ABCD中，若O四面体ABCD内任意点存在什么类似的命题
VO-BCD
VABCD
+
V0-ABD
VABCD
+
VO-ACD
VABCD
+
VO-ABC
VABCD
=1
VO-BCD
VABCD
+
V0-ABD
VABCD
+
VO-ACD
VABCD
+
VO-ABC
VABCD
=1
．
在△ABC中，角A，B，C的对边分别为a，b，c，已知向量
m
=（2a-c，b）与向量
n
=（cosB，-cosC）互相垂直．
（1）求角B的大小；
（2）求函数y=2sin2C+cos（B-2C）的值域；
（3）若AB边上的中线CO=2，动点P满足
AP
=sin2θ•
AO
+cos2θ•
AC
(θ∈R)，求(
PA
+
PB
)•
PC
的最小值．
已知O是△ABC内任意一点，连接AO、BO、CO并延长交对边于A′、B′、C′，则
OA′
AA′
+
OB′
BB′
+
OC′
CC′
=1，运用类比猜想，对于空间中四面体A-BCD有
OA′
AA′
+
OB′
BB′
+
OC′
CC′
+
OD′
DD′
=1
OA′
AA′
+
OB′
BB′
+
OC′
CC′
+
OD′
DD′
=1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网