题目内容
(本小题16分)函数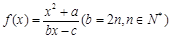 的定义域为{x| x ≠1},图象过原点,且
的定义域为{x| x ≠1},图象过原点,且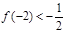 .
.
(1)试求函数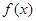 的单调减区间;
的单调减区间;
(2)已知各项均为负数的数列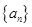 前n项和为
前n项和为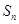 ,满足
,满足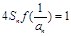 ,
,
求证: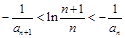 ;
;
【答案】
解:(1)由己知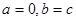 .
.
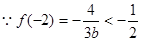 且
且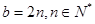
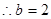
∴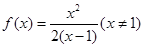 。。。。。。。。。。。。。。。。。。。。。。。4
。。。。。。。。。。。。。。。。。。。。。。。4
于是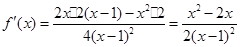
由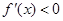 得
得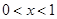 或
或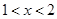
故函数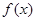 的单调减区间为
的单调减区间为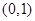 和
和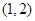 .。。。。。。。。。。。。。。。。6
.。。。。。。。。。。。。。。。。6
(2)由已知可得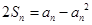 ,
,
当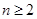 时,
时,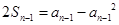
两式相减得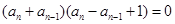
∴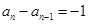 (各项均为负数)
(各项均为负数)
当 时,
时,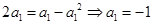 ,
∴
,
∴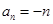 。。。。。。。。。。。8
。。。。。。。。。。。8
于是,待证不等式即为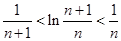 .
.
为此,我们考虑证明不等式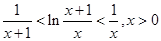 .。。。。。。。。。。。10
.。。。。。。。。。。。10
令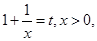 则
则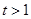 ,
,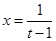
再令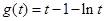 ,
,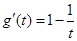 由
由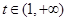 知
知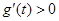
∴当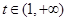 时,
时,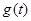 单调递增 ∴
单调递增 ∴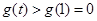 于是
于是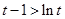
即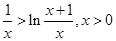 ①.。。。。。。。。。。。。。。。。。。。。。。。。。。12
①.。。。。。。。。。。。。。。。。。。。。。。。。。。12
令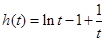 ,
,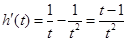 由
由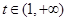 知
知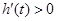
∴当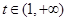 时,
时,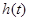 单调递增 ∴
单调递增 ∴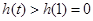 于是
于是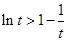
即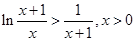 ②.。。。。。。。。。。。。。。。。。。。。。。。14
②.。。。。。。。。。。。。。。。。。。。。。。。14
由①、②可知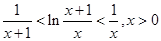
所以,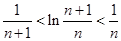 ,即
,即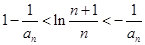 .。。。。。。。。。。。。。。。。16
.。。。。。。。。。。。。。。。。16
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
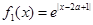 ,
,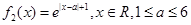 。
。 ,求使
,求使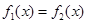 的
的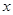 的值;
的值;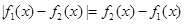 对于任意的实数
对于任意的实数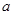 的取值范围;
的取值范围;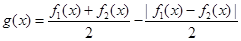 在
在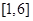 上的最小值.
上的最小值.