题目内容
已知向量 =(sinx,1+cos2x),
=(sinx,1+cos2x), =(sinx-cosx,cos2x+
=(sinx-cosx,cos2x+ ),定义函数f(x)=
),定义函数f(x)= •(
•( -
-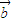 )
)(Ⅰ)求函数f(x)最小正周期;
(Ⅱ)在△ABC中,角A为锐角,且
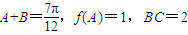 ,求边AC的长.
,求边AC的长.
【答案】分析:(Ⅰ)先根据向量的减法运算求出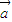 -
-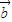 ,根据题中的新定义及平面向量的数量积的运算法则表示出f(x),然后利用二倍角的正弦函数公式及两角和的正弦函数公式化为一个角的正弦函数,然后利用周期公式T=
,根据题中的新定义及平面向量的数量积的运算法则表示出f(x),然后利用二倍角的正弦函数公式及两角和的正弦函数公式化为一个角的正弦函数,然后利用周期公式T= 即可求出f(x)的最小正周期;
即可求出f(x)的最小正周期;
(Ⅱ)根据f(A)=1,由第一问求出的f(x)的解析式,根据A的范围,利用特殊角的三角函数值求出A的度数,再根据A+B的度数求出B的度数,由已知的BC,sinA及sinB的值,利用正弦定理即可求出AC的值.
解答:解:(Ⅰ)
=
∴ ;(6分)
;(6分)
(Ⅱ)由f(A)=1得 ,
,
∴ 且
且 ,
,
∴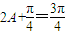 ,解得
,解得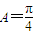 ,
,
又∵ ,∴
,∴ ,(10分)
,(10分)
在△ABC中,由正弦定理得: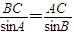 ,
,
∴ .(12分)
.(12分)
点评:此题综合考查了三角函数的恒等变换,正弦定理及平面向量的数量积运算.函数周期的求法是把函数化为一个角的三角函数,然后利用周期公式求出.熟练掌握三角函数公式及平面向量的运算法则是解本题的关键.
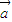 -
-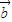 ,根据题中的新定义及平面向量的数量积的运算法则表示出f(x),然后利用二倍角的正弦函数公式及两角和的正弦函数公式化为一个角的正弦函数,然后利用周期公式T=
,根据题中的新定义及平面向量的数量积的运算法则表示出f(x),然后利用二倍角的正弦函数公式及两角和的正弦函数公式化为一个角的正弦函数,然后利用周期公式T= 即可求出f(x)的最小正周期;
即可求出f(x)的最小正周期;(Ⅱ)根据f(A)=1,由第一问求出的f(x)的解析式,根据A的范围,利用特殊角的三角函数值求出A的度数,再根据A+B的度数求出B的度数,由已知的BC,sinA及sinB的值,利用正弦定理即可求出AC的值.
解答:解:(Ⅰ)

=

∴
 ;(6分)
;(6分)(Ⅱ)由f(A)=1得
 ,
,∴
 且
且 ,
,∴
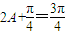 ,解得
,解得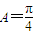 ,
,又∵
 ,∴
,∴ ,(10分)
,(10分)在△ABC中,由正弦定理得:
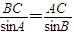 ,
,∴
 .(12分)
.(12分)点评:此题综合考查了三角函数的恒等变换,正弦定理及平面向量的数量积运算.函数周期的求法是把函数化为一个角的三角函数,然后利用周期公式求出.熟练掌握三角函数公式及平面向量的运算法则是解本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知向量
=(sinx,cosx),向量
=(1,
),则|
+
|的最大值为( )
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |