题目内容
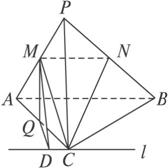
如图，在三棱锥
中，
平面
，
，
为侧棱
上一点，它的正（主）视图和侧（左）视图如图所示．
（1）证明：
平面
；
（2）求三棱锥
的体积；
（3）在
的平分线上确定一点
，使得
平面
，并求此时
的长．
【答案】
（1）因为
平面
，所以
，
又
，所以
平面
，所以
．
由三视图可得，在
中，
，
为
中点，所以
，
所以
平面
，
（2）由三视图可得
，[来源:学|科|网Z|X|X|K]
由⑴知
，平面，
又三棱锥
的体积即为三棱锥
的体积，
所以，所求三棱锥的体积
．
（3）取
的中点
，连接
并延长至
，使得
，点即为所求．
因为为
中点，所以
，
因为
平面
，
平面，所以
平面，
连接
，
，四边形
的对角线互相平分，
所以为平行四边形，所以
，又平面，
所以在直角
中，
．
【解析】略
练习册系列答案
阅读快车系列答案
相关题目
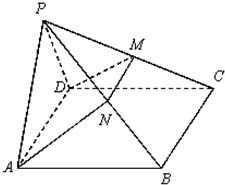如图，在四棱锥P-ABCD中，侧面PAD是正三角形，且与底面ABCD垂直，底面ABCD是边长为2的菱形，∠BAD=60°，N是PB中点，过A、N、D三点的平面交PC于M．
（2013•青岛一模）如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，N是PB中点，过A、N、D三点的平面交PC于M．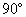
，∠B=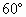
，PC⊥平面ABC，AB=8，PC=6，M，N分别是PA，PB的中点，设△MNC所在平面与△ABC所在平面交于直线l．(1)判断l与MN的位置关系；(2)求点M到l的距离．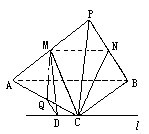
如图，在四棱锥
中，侧面
垂直，底面
，
是
中点，过
、
三点的平面交
于
． 
； (2)求证：
中点；(3)求证：平面
⊥平面
.