题目内容
已知数列{a![]() }满足a
}满足a![]() =1,a
=1,a![]() =2a
=2a![]() +1(n∈N
+1(n∈N![]() )
)
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列满足4k1-14k2-1…4k-1=(an+1)km(n∈N*),证明: ![]() 是等差数列;
是等差数列;![]()
(Ⅲ)证明:![]() (n∈N*).
(n∈N*).
(I)解:∵an+1=2 an+1(n∈N),
∴an+1+1=2(an+1),
∴| an+1| 是以a1+1=2为首项,2为公比的等比数列。
∴an+1=2n,
既an=2n-1(n∈N)。
(II)证法一:∵4b1-14 b2-2…4 bn-1=(a+1)bn,
∵4k1+k2+…+kn =2nk,
∴2[(b1+b2+…+bn)-n]=nb, ①
2[(b1+b2+…+bn+1)-(n+1)]=(n+1)bn+1 ②
②-①,得2(bn+1-1)=(n+1)bn+1-nb,
即 (n-1)bn+1-nbn+2=0. ③
nbn+2=(n+1)bn+1+2=0. ④
④-③,得nbn+2-2nbn+1-nbn=0,
即 bn+2-2bn+1+b=0,
∴bn-2-bn+1=bn(n∈N*),
∴{bn}是等差数列.
证法二:同证法一,得
(n-1)bn+1=nbn+2=0
令n=1,得b1=2.
设b2=2+d(d∈R),,下面用数学归纳法证明 bn=2+(n-1)d.
(1)当n=1,得b1=2.
(2)假设当n=k(k≥2)时,b1=2+(k-1)d,那么
bk+1=![]()
这就是说,当n=k+1时,等式也成立.
根据(1)和(2),可知bn=2(n-1)d对任何n∈N*都成立.
∵bn+1-bn=d, ∴{bn}是等差数列.
(3)证明:∵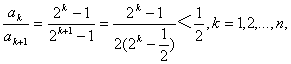
∴![]()
∵![]() ≥
≥![]() (
(![]() ),k=1,2,…,n,
),k=1,2,…,n,

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案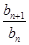 =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )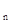 }满足a
}满足a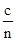 ,若对所有n
,若对所有n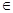 N
N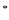 不等式a
不等式a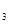 恒成立,则实数c的取值范围是_____________;
恒成立,则实数c的取值范围是_____________;