题目内容
已知焦点在y轴上的椭圆方程为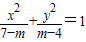
，则m的范围为（ ）A．（4，7）
B．（5.5，7）
C．（7，+∞）
D．（-∞，4）
【答案】分析：利用椭圆焦点在y轴上，可得不等式，从而可求m的范围．
解答：解：由题意，m-4＞7-m＞0，∴5.5＜m＜7
∴m的范围为（5.5，7）
故选B．
点评：本题考查椭圆的标准方程，考查学生的计算能力，属于基础题．
解答：解：由题意，m-4＞7-m＞0，∴5.5＜m＜7
∴m的范围为（5.5，7）
故选B．
点评：本题考查椭圆的标准方程，考查学生的计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知椭圆C的中心在原点O，焦点在
轴上，长轴长是短轴
长的2倍，且经过点M
.
平行于OM的直线
在
轴上的截距为
并交椭
圆C于A、B两个不同点.
（1）求椭圆C的标准方程；
（2）求的取值范围；
|
轴始终围成一个等腰三角形.
的椭圆，使两端点A、B恰好重合于椭圆的一个短轴端点，如图2；再将这个椭圆放在平面直角坐标系中，使其中心在坐标原点，长轴在x轴上，已知此时点A的坐标为（0，1），如图3，在图形变化过程中，图1中线段AM的长度对应于图3中的椭圆弧ADM的长度．图3中直线AM与直线y=-2交于点N（n，-2），则与实数m对应的实数就是n，记作f（m）=n，
；②函数f（m）是奇函数；③函数f（m）在（0，k）上单调递增；④函数f（m）的图象关于点
对称；⑤函数
时AM过椭圆的右焦点．其中所有的真命题是（ ）