题目内容
(本小题满分8分)下面三条直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4不能构成三角形.求m的取值范围.
m=-1,-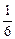 ,
,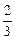 ,4.
,4.
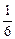 ,
,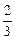 ,4.
,4.三条直线既不共点又不平行才能构成三角形.
(1)三直线共点时,由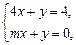
解得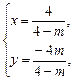 代入l3得m=
代入l3得m=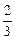 或m=-1.
或m=-1.
(2)至少两条直线平行或重合时,l1、l2、l3至少两条直线斜率相等.
∵k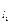 =-4,k
=-4,k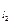 =-m,k
=-m,k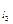 =
=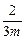 ,
,
∴-4=-m或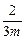 =-4或-m=
=-4或-m=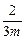 .
.
∴m=4或m=-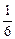 .
.
综合(1)(2)可知m=-1,-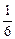 ,
,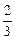 ,4.
,4.
(1)三直线共点时,由
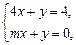
解得
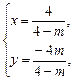 代入l3得m=
代入l3得m=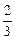 或m=-1.
或m=-1.(2)至少两条直线平行或重合时,l1、l2、l3至少两条直线斜率相等.
∵k
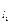 =-4,k
=-4,k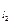 =-m,k
=-m,k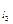 =
=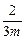 ,
,∴-4=-m或
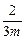 =-4或-m=
=-4或-m=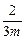 .
.∴m=4或m=-
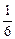 .
.综合(1)(2)可知m=-1,-
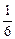 ,
,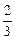 ,4.
,4.
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 与直线m是异面直线,直线
与直线m是异面直线,直线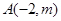 和
和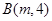 的直线与直线
的直线与直线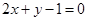 平行,则
平行,则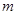 的值为( )
的值为( )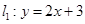 ,直线
,直线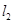 与
与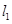 关于直线
关于直线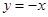 对称,则直线
对称,则直线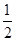
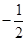
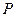 是⊙
是⊙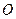 :
: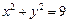 上的任意一点,过
上的任意一点,过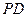 垂直
垂直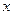 轴于
轴于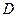 ,动点
,动点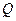 满足
满足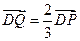 。
。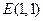 ,在动点
,在动点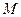 、
、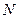 ,使
,使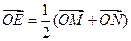 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线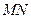 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。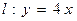 和点
和点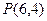 ,点
,点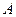 为第一象限内的点且在直线
为第一象限内的点且在直线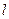 上,直线
上,直线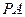 交
交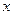 轴正半轴于点
轴正半轴于点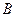 ,求△
,求△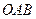 面积的最小值,并求当△
面积的最小值,并求当△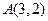 且垂直于直线
且垂直于直线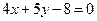 的直线方程为
的直线方程为  与
与 平行,则
平行,则 等于( )
等于( )