题目内容
 在直角梯形PBCD中,∠D=∠C=
在直角梯形PBCD中,∠D=∠C=| π |
| 2 |
| SE |
| 1 |
| 3 |
| SD |
(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求二面角E-AC-D的正切值.
分析:(法一)(1)由题意可知,翻折后的图中SA⊥AB①,易证BC⊥SA②,由①②根据直线与平面垂直的判定定理可得SA⊥平面ABCD;
(2)(三垂线法)由
=
考虑在AD上取一点O,使得
=
,从而可得EO∥SA,所以EO⊥平面ABCD,过O作OH⊥AC交AC于H,连接EH,∠EHO为二面角E-AC-D的平面角,在Rt△AHO中求解即可
(法二:空间向量法)
(1)同法一
(2)以A为原点建立直角坐标系,易知平面ACD的法向为
=(0,0,2),求平面EAC的法向量,代入公式求解即可
(2)(三垂线法)由
| SE |
| 1 |
| 3 |
| SD |
| AO |
| 1 |
| 3 |
| AD |
(法二:空间向量法)
(1)同法一
(2)以A为原点建立直角坐标系,易知平面ACD的法向为
| AS |
解答:解法一:(1)证明:在题平面图形中,由题意可知,BA⊥PD,ABCD为正方形,
所以在翻折后的图中,SA⊥AB,SA=2,四边形ABCD是边长为2的正方形,
因为SB⊥BC,AB⊥BC,SB∩AB=B
所以BC⊥平面SAB,
又SA?平面SAB,
所以BC⊥SA,
又SA⊥AB,BC∩AB=B
所以SA⊥平面ABCD,
(2)在AD上取一点O,使
=
,连接EO
因为
=
,所以EO∥SA
因为SA⊥平面ABCD,
所以EO⊥平面ABCD,
过O作OH⊥AC交AC于H,连接EH,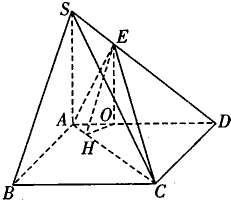
则AC⊥平面EOH,
所以AC⊥EH.
所以∠EHO为二面角E-AC-D的平面角,EO=
SA=
.
在Rt△AHO中,∠HAO=45°,HO=AO•sin45°=
×
=
∴tan∠EHO=
=2
,
即二面角E-AC-D的正切值为2
解法二:(1)同方法一
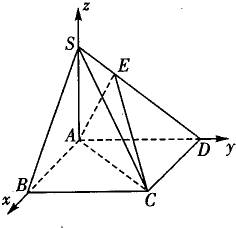
(2)解:如图,以A为原点建立直角坐标系,A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),S(0,0,2),E(0,
,
)
∴平面ACD的法向为
=(0,0,2)
设平面EAC的法向量为
=(x,y,z),
=(2,2,0),
=(0,
,
)
由
,
所以
,可取
所以
=(2,-2,1).
所以cos<
,
>=
=
=
所以tan<
,
>=2
即二面角E-AC-D的正切值为2
所以在翻折后的图中,SA⊥AB,SA=2,四边形ABCD是边长为2的正方形,
因为SB⊥BC,AB⊥BC,SB∩AB=B
所以BC⊥平面SAB,
又SA?平面SAB,
所以BC⊥SA,
又SA⊥AB,BC∩AB=B
所以SA⊥平面ABCD,
(2)在AD上取一点O,使
| AO |
| 1 |
| 3 |
| AD |
因为
| SE |
| 1 |
| 3 |
| SD |
因为SA⊥平面ABCD,
所以EO⊥平面ABCD,
过O作OH⊥AC交AC于H,连接EH,

则AC⊥平面EOH,
所以AC⊥EH.
所以∠EHO为二面角E-AC-D的平面角,EO=
| 2 |
| 3 |
| 4 |
| 3 |
在Rt△AHO中,∠HAO=45°,HO=AO•sin45°=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∴tan∠EHO=
| EO |
| OH |
| 2 |
即二面角E-AC-D的正切值为2
| 2 |
解法二:(1)同方法一
(2)解:如图,以A为原点建立直角坐标系,A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),S(0,0,2),E(0,
| 2 |
| 3 |
| 4 |
| 3 |
∴平面ACD的法向为
| AS |
设平面EAC的法向量为
| n |
| AC |
| AE |
| 2 |
| 3 |
| 4 |
| 3 |

由
|
所以
|
|
所以
| n |
所以cos<
| n |
| AS |
| ||||
|
|
| 2 |
| 2×3 |
| 1 |
| 3 |
所以tan<
| n |
| AS |
| 2 |
即二面角E-AC-D的正切值为2
| 2 |
点评:本题以平面图形的翻折为载体,考查空间直线与平面的位置关系:直线与平面平行及直线与平面平行的判定定理的运用,空角角中的二面角的平面角的作法及求解,利用向量的方法求解空间距离及空间角的方法,两法并举,注意细细体会.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
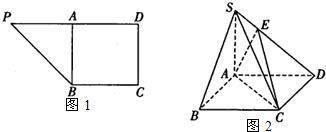 在直角梯形PBCD中,∠D=∠C=
在直角梯形PBCD中,∠D=∠C=
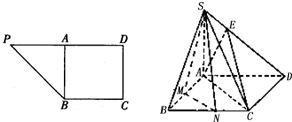
 ,将
,将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下右图。
,如下右图。 平面ABCD;(2)求二面角E—AC—D的正切值.
平面ABCD;(2)求二面角E—AC—D的正切值.