题目内容
21. 双曲线C与椭圆![]() 有相同的焦点,直线y=
有相同的焦点,直线y=![]() x为C的一条渐近线.
x为C的一条渐近线.
(Ⅰ)求双曲线C的方程;
(Ⅱ)过点P(0,4)的直线l,交双曲线C于A、B两点,交x轴于Q点(Q点与C的顶点不重合).当![]() =λ1
=λ1![]() =λ2
=λ2![]() ,且λ1+λ2=
,且λ1+λ2=![]() 时,求Q点的坐标.
时,求Q点的坐标.
解:(Ⅰ)设双曲线方程为![]() =1.
=1.
由椭圆![]() 求得两焦点为(-2,0),(2,0).
求得两焦点为(-2,0),(2,0).
∴对于双曲线C:c=2.又y=![]() x为双曲线C的一条渐近线,
x为双曲线C的一条渐近线,
∴![]() 解得 a2=1,b2=3,
解得 a2=1,b2=3,
∴双曲线C的方程为: ![]() -
-![]() =1.
=1.
(Ⅱ)解法一:
由题意知直线l的斜率k存在且不等于零.
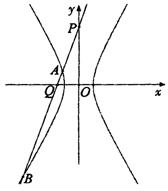
设l的方程:y=kx+4,A(x1,y1),
B(x2,y2),
则Q(-![]() ,0),
,0),
∵![]() =λ1
=λ1![]() ,
,
∴(-![]() ,-4)=λ1(x1+
,-4)=λ1(x1+![]() ,y1).
,y1).
∴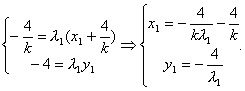
∵A(x1,y1)在双曲线C上,
∴![]() =0.
=0.
∴![]() .
.
∴![]()
同理有:(16-k2)λ22+32λ2+16-![]() k2=0.
k2=0.
若16-k2=0,则直线l过顶点,不合题意. ∴16-k2≠0.
∴λ1、λ2是二次方程(16-k2)x2+32x+16-![]() k2=0的两根.
k2=0的两根.
∴λ1+λ2=![]() .
.
∴k2=4,
此时△>0, ∴k=±2.
∴所求Q的坐标为(±2,0).
解法二:
由题意知直线l的斜率k存在且不等于零
设l的方程: y=kx+4,A(x1,y1),B(x2,y2),则Q(-![]() ,0).
,0).
∵![]() =λ1
=λ1![]() ,
,
∴Q分![]() 的比为λ1.
的比为λ1.
由定比分点坐标公式得:
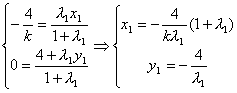
下同解法一
解法三:
由题意知直线l的斜率k存在且不等于零.
设l的方程: y=kx+4,A(x1,y1),B(x2,y2), 则Q(-![]() ,0).
,0).
∵![]() =λ1
=λ1![]() =λ2
=λ2![]() ,
,
∴(-![]() ,-4)=λ1(x1+
,-4)=λ1(x1+![]() ,y1)=λ2(x2+
,y1)=λ2(x2+![]() ,y2).
,y2).
∴-4=λ1yl=λ2y2.
∴λ1=-![]() ,λ2=-
,λ2=-![]() .
.
又λ1+λ2=-![]() ,
,
∴![]() .
.
即 3(y1+y2)=2y1y2.
将y=kx+4代入x2-![]() =1得
=1得
(3-k2)y2-24y+48-3k2=0.
∵3-k2≠0,否则l与渐近线平行,
∴y1+y2=![]() ,y1y2=
,y1y2=![]() .
.
∴![]() .
.
∴k=±2.
∴Q(±2,0).


 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为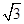 .
. 的方程;
的方程;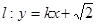 与双曲线
与双曲线 和
和 ,且
,且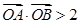
 为原点),求
为原点),求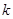 的取值范围.
的取值范围.