题目内容
求证: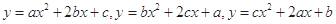 (
(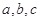 是互不相等的实数),三条抛物线至少有一条与
是互不相等的实数),三条抛物线至少有一条与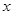 轴有两个交点.
轴有两个交点.
【答案】
证明 略.
【解析】采用反证法:假设这三条抛物线全部与x轴只有一个交点或没有交点,则有
 三式相加,可得到(a-b)2+(b-c)2+(c-a)2≤0,因为a,b,c是互不相等,所以此式不成立.问题得证
三式相加,可得到(a-b)2+(b-c)2+(c-a)2≤0,因为a,b,c是互不相等,所以此式不成立.问题得证

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
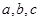 是互不相等的实数,
是互不相等的实数,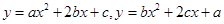 和
和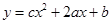 确定的三条抛物线至少有一条与
确定的三条抛物线至少有一条与 轴有两个不同的交点.
轴有两个不同的交点.