Question

【题目】如图所示，在正方体ABCD－A′B′C′D′中：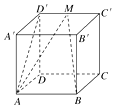

（1）求二面角D′－AB－D的大小；
（2）若M是C′D′的中点，求二面角M－AB－D的大小．

Answer 1

【答案】
（1）解：在正方体ABCD－A′B′C′D′中，AB⊥平面ADD′A′，所以AB⊥AD′，AB⊥AD，因此∠D′AD为二面角D′－AB－D的平面角，在Rt△D′DA中，∠D′AD＝45°，所以二面角D′－AB－D的大小为45°

（2）解：因为M是C′D′的中点，所以MA＝MB，取AB的中点N，连接MN，则MN⊥AB.取CD的中点H，连接HN，则HN⊥AB.

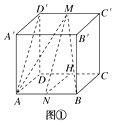
从而∠MNH是二面角M－AB－D的平面角．∠MNH＝45°，所以二面角M－AB－D的大小为45°.

【解析】(1)利用正方体的性质结合已知条件可得出线面垂直进而找到二面角D′－AB－D的平面角，再利用解三角形的知识求出平面角的大小进而得出二面角的大小。(2)由已知条件作出辅助线借助正方体的性质可找到∠MNH是二面角M－AB－D的平面角，根据已知条件即可求出平面角的大小故可得二面角的大小。
【考点精析】根据题目的已知条件，利用直线与平面垂直的性质的相关知识可以得到问题的答案，需要掌握垂直于同一个平面的两条直线平行．