题目内容
已知函数: ,
,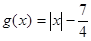 .
.
⑴解不等式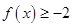 ;
;
⑵若对任意的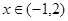 ,
,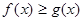 ,求
,求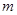 的取值范围.
的取值范围.
 ,
,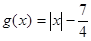 .
.⑴解不等式
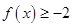 ;
;⑵若对任意的
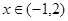 ,
,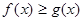 ,求
,求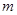 的取值范围.
的取值范围.(1) ①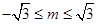 时,不等式的解为R; ②
时,不等式的解为R; ②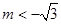 或
或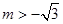 时,
时,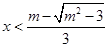 或
或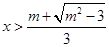 ;(2)
;(2)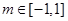 .
.
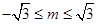 时,不等式的解为R; ②
时,不等式的解为R; ②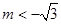 或
或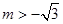 时,
时,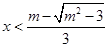 或
或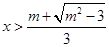 ;(2)
;(2)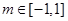 .
.试题分析:(1)含参数的二次不等式的解法要考虑判别式的值.(2)本题较难就是绝对值的处理,把x的范围按正负分开在讨论,特别是小于零部分的处理要细心,应用基本不等式的知识.
试题解析:⑴
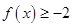 可化为
可化为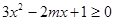 ,
,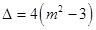 ,
,①当
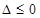 时,即
时,即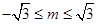 时,不等式的解为R;
时,不等式的解为R;②当
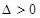 时,即
时,即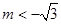 或
或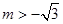 时,
时,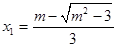 ,
, ,
,不等式的解为
 或
或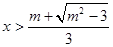 ;
;⑵
 ,对任意的
,对任意的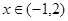 恒成立,
恒成立,①当
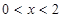 时,
时,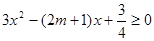 ,即
,即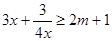 在
在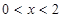 时恒成立;
时恒成立;因为
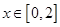 ,当
,当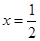 时等号成立.所以
时等号成立.所以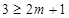 ,即
,即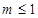 ;
; ②当
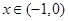 时,
时,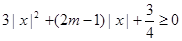 ,即
,即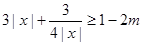 在
在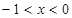 时恒成立,
时恒成立,因为
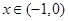 ,当
,当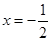 时等号成立.
时等号成立.所以
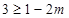 ,即
,即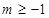 ;
;③当
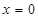 时,
时,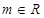 .综上所述,实数
.综上所述,实数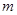 的取值范围是
的取值范围是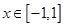 .
.
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
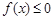 的解集为
的解集为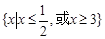 ,则
,则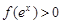 的解集为( )
的解集为( )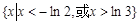
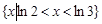
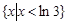 }
}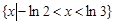
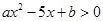 的解集为
的解集为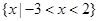 ,则不等式
,则不等式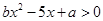 的解集为( )
的解集为( )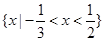
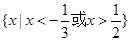
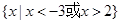
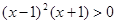 的解集为__________.
的解集为__________.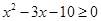 的解集是( )
的解集是( )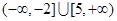
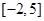

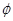
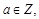 关于
关于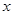 的一元二次不等式
的一元二次不等式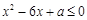 的解集中有且仅有3个整数,则所有符合条件的
的解集中有且仅有3个整数,则所有符合条件的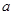 的值之和是( )
的值之和是( )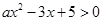 的解集为
的解集为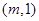 ,则实数
,则实数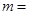 .
.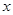 的不等式
的不等式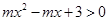 的解集为
的解集为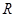 ,则实数
,则实数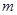 的取值范围是
的取值范围是