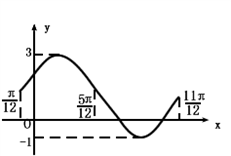
题目内容
 如图,是函数f1(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
如图,是函数f1(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<| π |
| 2 |
(Ⅰ)求函数f1(x)的解析式;
(Ⅱ)将函数y=f1(x)的图象按向量
| a |
| π |
| 4 |
分析:(1)欲求函数的解析式,关键是求出解析式中的四个变量A,B,ω,φ,这些量都可根据图象得到,ω可由周期得到,A,B
可由最大最小值得到,等等;
(2)欲求函数的最大值,必先要求出此函数的解析式,再根据三角函数的性质解得.
可由最大最小值得到,等等;
(2)欲求函数的最大值,必先要求出此函数的解析式,再根据三角函数的性质解得.
解答:解:(I)由图知:2A=3-(-1)=4,得A=2;
由A+B=3,得B=1;T=
-(-
)=π,于是ω=
=2
设f1(x)=2sin(2x+?)+1
将函数f(x)=2sin2x+1的图象向左平移
,得f1(x)=2sin(2x+?)+1的图象,
则?=2×
=
,
∴f1(x)=2sin(2x+
)+1(8分)
(II)依题意:f2(x)=2sin[2(x-
)+
]+1-2=-2cos(2x+
)-1
∴y=2sin(2x+
)-2cos(2x+
)=2
sin(2x-
)
当2x-
=2kπ+
,即x=kπ+
,k∈Z时,ymnx=2
此时x的取值集合为{x|x=kπ+
,k∈Z}(13分)
由A+B=3,得B=1;T=
| 11π |
| 12 |
| π |
| 12 |
| 2π |
| T |
设f1(x)=2sin(2x+?)+1
将函数f(x)=2sin2x+1的图象向左平移
| π |
| 12 |
则?=2×
| π |
| 12 |
| π |
| 6 |
∴f1(x)=2sin(2x+
| π |
| 6 |
(II)依题意:f2(x)=2sin[2(x-
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
∴y=2sin(2x+
| π |
| 6 |
| π |
| 6 |
| 2 |
| π |
| 12 |
当2x-
| π |
| 12 |
| π |
| 2 |
| 7π |
| 24 |
| 2 |
此时x的取值集合为{x|x=kπ+
| 7π |
| 24 |
点评:本题考查了由三角函数的图象求解析式的问题以及三角函数的图象与性质,属于中档题.三角函数的单调性与最大最小值问题是函数的重要性质,合理使用函数的性质,正确理解它们的含义,是熟练利用这些基本性质解综合问题的前提.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
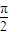 ,B∈R)在同一个周期内的图象.
,B∈R)在同一个周期内的图象. 平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.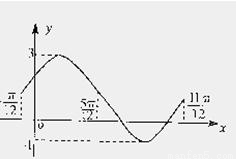
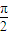 ,B∈R)在同一个周期内的图象.
,B∈R)在同一个周期内的图象. 平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
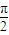 ,B∈R)在同一个周期内的图象.
,B∈R)在同一个周期内的图象. 平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.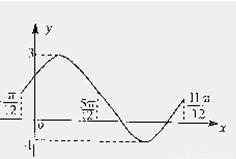
 ,B∈R)在同一个周期内的图象.
,B∈R)在同一个周期内的图象. 平移,得到函数y=f2(x),
平移,得到函数y=f2(x),