题目内容
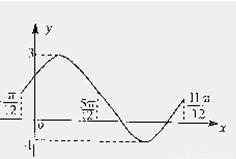
如图，是函数f1（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜
，B∈R）在同一个周期内的图象．
（I）求函数f1（x）的解析式；
（II）将函数y=f1（x）的图象按向量
平移，得到函数y=f2（x），
求y=f1（x）+f2（x）的最大值，并求此时自变量x的集合．
，B∈R）在同一个周期内的图象．（I）求函数f1（x）的解析式；
（II）将函数y=f1（x）的图象按向量
平移，得到函数y=f2（x），求y=f1（x）+f2（x）的最大值，并求此时自变量x的集合．
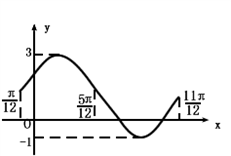
解：（I）由图知：2A=3﹣（﹣1）=4，得A=2；
由A+B=3，得B=1；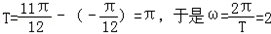
设f1（x）=2sin（2x+φ）+1
将函数f（x）=2sin2x+1的图象向左平移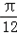
，得f1（x）=2sin（2x+φ）+1的图象，
则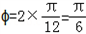
，
∴
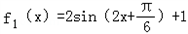
（II）依题意：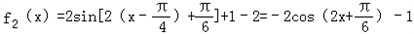
∴
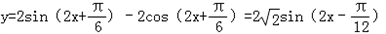
当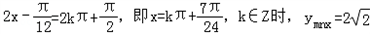
此时x的取值集合为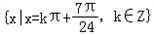
由A+B=3，得B=1；
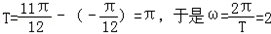
设f1（x）=2sin（2x+φ）+1
将函数f（x）=2sin2x+1的图象向左平移
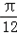，得f1（x）=2sin（2x+φ）+1的图象，则
，∴
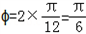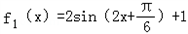
（II）依题意：
∴
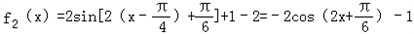
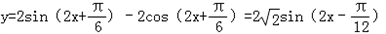
当
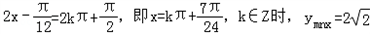
此时x的取值集合为
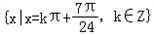
练习册系列答案
同步练习强化拓展系列答案
相关题目
如图，是函数f1（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜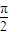
，B∈R）在同一个周期内的图象．
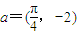平移，得到函数y=f2（x），求y=f1（x）+f2（x）的最大值，并求此时自变量x的集合．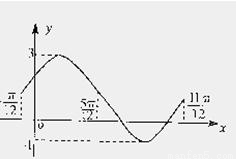
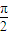，B∈R）在同一个周期内的图象．
平移，得到函数y=f2（x），求y=f1（x）+f2（x）的最大值，并求此时自变量x的集合．
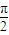，B∈R）在同一个周期内的图象．
平移，得到函数y=f2（x），求y=f1（x）+f2（x）的最大值，并求此时自变量x的集合．