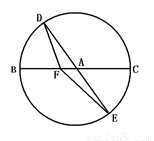
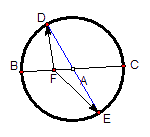
题目内容
如图，BC是单位圆A的一条直径，F是线段AB上的点，且
=2
，若DE是圆A中绕圆心A转动的一条直径，则
•
的值是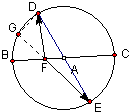
| BF |
| FA |
| FD |
| FE |
-
| 8 |
| 9 |
-
．| 8 |
| 9 |
分析：利用向量的运算法则将
，
分别用
，
与
，
表示，利用向量的运算律求出数量积的值即可求出所求．
| FD |
| FE |
| FA |
| AD |
| FA |
| AE |
解答：解：∵
=
+
，
=
+
，
∴
•
=（
+
）（
+
）
=
2+
•（
+
）+
•
，
∵
=2
，DE是圆A中绕圆心A转动的一条直径，
∴
+
=
，
•
=-1，|
|=
|
|=1
∴
•
=
+0-1=-
．
故答案为：-
．
| FD |
| FA |
| AD |
| FE |
| FA |
| AE |
∴
| FD |
| FE |
| FA |
| AD |
| FA |
| AE |
=
| FA |
| FA |
| AD |
| AE |
| AD |
| AE |
∵
| BF |
| FA |
∴
| AD |
| AE |
| 0 |
| AD |
| AE |
| FA |
| 1 |
| 3 |
| AB |
∴
| FD |
| FE |
| 1 |
| 9 |
| 8 |
| 9 |
故答案为：-
| 8 |
| 9 |
点评：求向量的数量积，一般应该先将各个未知的向量利用已知向量线性表示，再利用向量的运算律展开，转化为已知向量的数量积求出值．属于中档题．
练习册系列答案
相关题目
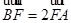，若DE是圆A中绕圆心A转动的一条直径，则
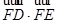的值是 。
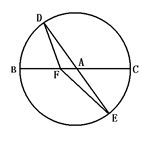
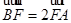，若DE是圆A中绕圆心A转动的一条直径，则
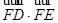的值是 。
，若DE是圆A中绕圆心A运动的一条直径，则
的值是 （ ）
B. 
C. 
D. 不确定