题目内容
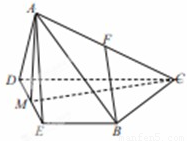
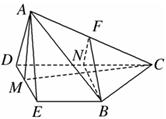
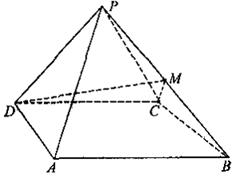
如图,四棱锥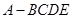 中,侧面
中,侧面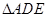 是等边三角形,在底面等腰梯形
是等边三角形,在底面等腰梯形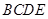 中,
中,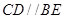 ,
,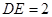 ,
,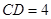 ,
,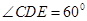 ,
,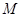 为
为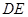 的中点,
的中点,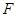 为
为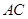 的中点,
的中点,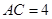 .
.
(1)求证:平面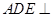 平面
平面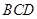 ;
;
(2)求证: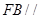 平面
平面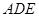 .
.
【答案】
(1)证明过程详见解析;(2)证明过程详见解析.
【解析】
试题分析:本题主要以四棱锥为几何背景考查线线垂直、线面垂直、面面垂直、线面平行的判定,运用传统几何法证明,突出考查空间想象能力.第一问,利用已知的边长和特殊关系,证明出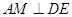 ,
,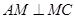 ,所以利用线面垂直的判定定理就会得出
,所以利用线面垂直的判定定理就会得出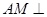 平面
平面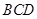 ,再利用面面垂直的判定定理即可;第二问,先利用线面平行的判定定理证明
,再利用面面垂直的判定定理即可;第二问,先利用线面平行的判定定理证明 ∥平面
∥平面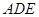 ,通过同位角相等可以得出
,通过同位角相等可以得出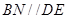 ,再证明
,再证明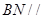 平面
平面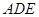 ,再通过面面平行的判定定理得到平面
,再通过面面平行的判定定理得到平面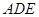 ∥平面
∥平面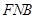 ,所以面内的线
,所以面内的线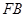 平行平面
平行平面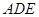 .
.
试题解析:(Ⅰ)∵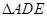 是等边三角形,
是等边三角形,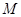 是
是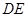 的中点,
的中点,
∴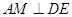 ,
,
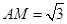 . 2分
. 2分
∵在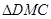 中
中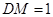 ,
,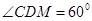 ,
,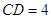 , 3分
, 3分
∴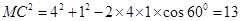 ,∴
,∴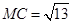 .
.
在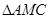 中,
中,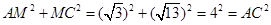 , 4分
, 4分
∴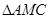 是直角三角形.∴
是直角三角形.∴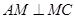 .
.
又∵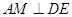 ,
,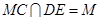 ,∴
,∴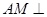 平面
平面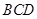 .
.
又∵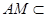 平面
平面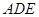 ,∴平面
,∴平面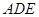 ⊥平面
⊥平面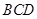 . 6分
. 6分
(Ⅱ)取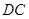 的中点
的中点 ,连接
,连接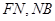 .
.
∵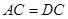 ,
,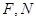 点分别是
点分别是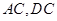 的中点,∴
的中点,∴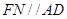 .
.
又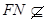 平面
平面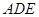 ,
,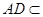 平面
平面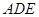 ,所以
,所以 ∥平面
∥平面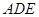 . 8分
. 8分
∵点 是
是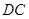 的中点,∴
的中点,∴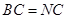 ,
,
又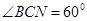 ,∴
,∴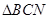 是等边三角形,∴
是等边三角形,∴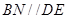 .
.
又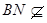 平面
平面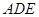 ,
,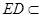 平面
平面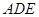 ,所以
,所以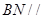 平面
平面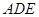 .
.
∵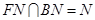 ,∴平面
,∴平面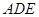 ∥平面
∥平面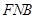 .
.
∵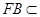 平面
平面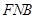 ,∴
,∴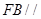 平面
平面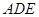 .
12分
.
12分
考点:1.余弦定理;2.勾股定理;3.线面垂直的判定定理;4.面面垂直的判定定理;5.线面平行的判定定理;6.面面平行的判定定理.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
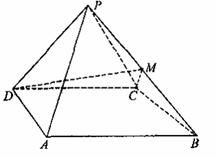
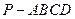 中,
中,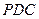 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面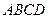 是
是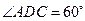 的菱形,
的菱形,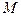 为
为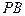 的中点.
的中点.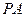 与底面
与底面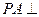 平面
平面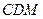 ;
;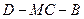 的余弦值.
的余弦值. 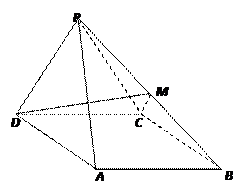
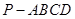 中,侧面
中,侧面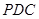 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面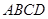 是
是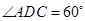 的菱形,
的菱形,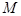 为
为 的中点.
的中点.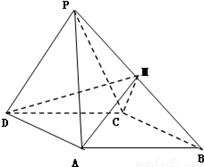
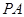 与底面
与底面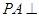 平面
平面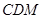 ;(Ⅲ)求二面角
;(Ⅲ)求二面角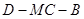 的余弦值.
的余弦值.  中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 