题目内容
19.四棱锥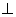
(Ⅰ)证明:![]() ;
;
(Ⅱ)求直线SD与平面SAB所成角的大小。
解:(Ⅰ)作![]() ,垂足为O,连结AO,由侧面SBC
,垂足为O,连结AO,由侧面SBC![]() 底面ABCD,得SO
底面ABCD,得SO![]() 底面ABCD
底面ABCD
因为SA=SB,所以AO=BO
又![]() 为等腰直角三角形,AO
为等腰直角三角形,AO![]() BO
BO
由三垂线定理,得SA![]() BC
BC
(Ⅱ)由(Ⅰ)知SA![]() BC,依题设AD
BC,依题设AD![]() BC
BC
故SA![]() AD,由AD=BC=
AD,由AD=BC=![]() ,SA=
,SA=![]() ,AO=
,AO=![]() ,得
,得
△SAB的面积![]() 。
。
连结DB,得△DAB的面积![]()
设D到平面SAB的距离为h ,由![]() ,得
,得![]() ,
,
解得![]()
设SD与平面SAB所成角为![]() ,则
,则![]()
所以,直线SD与平面SAB所成的角为![]() .
.

练习册系列答案
相关题目
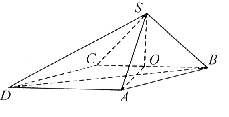
 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.
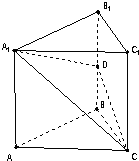
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C. 如图,在三棱锥P-ABC中,底面ABC为等腰直角三角形,∠ACB=90°,棱PA垂直底面ABC,PA=AB=4,BD=
如图,在三棱锥P-ABC中,底面ABC为等腰直角三角形,∠ACB=90°,棱PA垂直底面ABC,PA=AB=4,BD=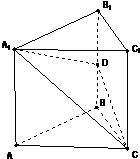 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.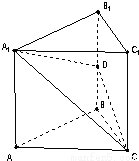 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.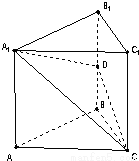 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C.