题目内容
 本题共3个小题,第1、2小题满分各5分,第3小题满分6分.
本题共3个小题,第1、2小题满分各5分,第3小题满分6分.如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”(点D在线段BC上),设AB长为a,BC长为b,∠BAD=θ.现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2的比值
| S1 |
| S2 |
(1)求证:正方形BEFG的边长为
| atanθ |
| 1+tanθ |
(2)将草花比y表示成θ的函数关系式;
(3)当θ为何值时,y有最小值?并求出相应的最小值.
分析:(1)设正方形BEFG的边长t,则AE=a-t,利用相似比建立等式,从而可以证明;
(2)由于题目中“设∠DAB=θ,”,故可利用解三角形的知识解决“草花比y”;
(3)设tanθ=x,则y=
(x+
)括号中两式的积是定值,故利用二元不等式求其最小值.
(2)由于题目中“设∠DAB=θ,”,故可利用解三角形的知识解决“草花比y”;
(3)设tanθ=x,则y=
| 1 |
| 2 |
| 1 |
| x |
解答:解:(1)设正方形BEFG的边长t,则AE=a-t,由
=
,得
=
(或:因为AE=tcoθ,a-t=tcoθ),解得t=
,(5分)
(2)BD=atanθ,△ABD的面积为
a2tanθ,S2=
则S1=
a2tanθ -S2=
a2tanθ-
(8分)
所以y=
=
-1(θ∈(0, arctan
])(10分)
(3)设tanθ=x,则y=
(x+
)
①当a≤b时,
≥1,x=1即θ=
时取最小值,最小值为1. (14分)
②当a>b时,x∈(0,
],
<1,y=
(x+
)是减函数,
所以当θ=arctan
时取最小值,最小值为
(
+
)(16分)
| FG |
| AB |
| DG |
| DB |
| t |
| a |
| atanθ-t |
| atanθ |
(或:因为AE=tcoθ,a-t=tcoθ),解得t=
| atanθ |
| 1+tanθ |
(2)BD=atanθ,△ABD的面积为
| 1 |
| 2 |
| a2tan2 θ |
| (1+tanθ)2 |
则S1=
| 1 |
| 2 |
| 1 |
| 2 |
| a2tan2θ |
| (1+tanθ)2 |
所以y=
| S1 |
| S2 |
| (1+tanθ)2 |
| 2tanθ |
| b |
| a |
(3)设tanθ=x,则y=
| 1 |
| 2 |
| 1 |
| x |
①当a≤b时,
| b |
| a |
| π |
| 4 |
②当a>b时,x∈(0,
| b |
| a |
| b |
| a |
| 1 |
| 2 |
| 1 |
| x |
所以当θ=arctan
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| a |
| b |
点评:本题的考点是在实际问题中建立三角函数模型,主要考查函数在实际生活中的应用、解三角形以及利用二元不等式求函数最值的方法,解决实际问题通常有几个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果,其中关键是建立数学模型.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
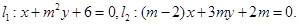 讨论当实数m为何值时,(1)
讨论当实数m为何值时,(1)
 称为“草花比y”.
称为“草花比y”.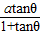 ;
;