题目内容
某体育项目的比赛规则,由三局两胜改为五局三胜的新赛制,由以往的经验,单场比赛甲胜乙的概率为![]() ,各局比赛相互之间没有影响。
,各局比赛相互之间没有影响。
(Ⅰ)依以往的经验,在新赛制下,求乙以3:2获胜的概率;
(Ⅱ)试用概率知识解释新赛制对谁更有利。
解:(Ⅰ)记![]() 表示事件:“在新赛制下,乙以
表示事件:“在新赛制下,乙以![]() :
:![]() 获胜”,则
获胜”,则![]()
因此,在新赛制下,乙以![]() :
:![]() 获胜的概率为
获胜的概率为![]() .
.
(Ⅱ)记B表示事件:“采用新赛制,乙获胜”,
B1表示事件:“采用新赛制,乙以3:0获胜”,
B2表示事件:“采用新赛制,乙以 3:1获胜”,
B3表示事件:“采用新赛制,乙以 3:2获胜”.
则,B= B1 + B2+ B3且 B1 , B2, B3彼此互斥,![]()
![]() ,
,
采取新赛制,乙获胜的概率P(B)=P(B1+ B2+ B3)=P(B1)+P(B2)+P(B3)
![]() .
.
记C示事件:“采取三局二胜制,乙获胜”,
同理,采取三局二胜制,乙获胜的概率![]()
![]() .
.
所以,采取新赛制对甲更有利.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
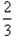 ,各局比赛相互之间没有影响。
,各局比赛相互之间没有影响。