题目内容
已知直线y=kx-1与双曲线x2-y2=1的左支交于A、B两点，若另一条直线l过点P(-2，0)及线段AB的中点Q，求直线l在y轴上的截距的取值范围.
解析：由方程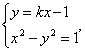
消去y,整理得
(1-k2)x2+2kx-2=0.
由题设得
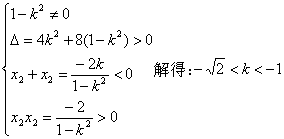
设A、B两点坐标分别为(x1,y1)、(x2,y2)
则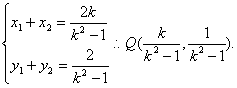
∴直线l的方程为y=
令x=0,得直线l在y轴上截距b=
∵-
＜k＜-1,
∴截距b的取值范围是：(-∞,-2)∪(2+
,+∞).
练习册系列答案
相关题目
（理）已知直线y=kx+1（k∈R）与椭圆
+
=1总有交点，则m的取值范围为（ ）
| x2 |
| 2 |
| y2 |
| m |
| A、（1，2] |
| B、[1，2） |
| C、[1，2）∪[2，+∞） |
| D、（2，+∞） |