题目内容

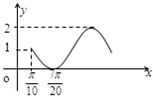精英家教网函数y=f（x）的图象如图所示，则y=f（x）的解析式为（　　）
A、y=sin2x-2
B、y=2cos3x-1
C、y=sin(2x-
π
5
)-1
D、y=1-sin(2x-
π
5
)
分析：本题可以使用排除法进行解答，根据函数图象分析出函数的最值，进而分析四个答案中四个函数的最值，将不符合条件的答案排除掉，即可得到正确的答案．
解答：解：由已知中函数的解析式，我们可得函数的最大值为2，最小值为0，
而A中函数y=sin2x-2，最大值为-1，最小值为-3，不满足要求，故A不正确；
B中函数y=2cos3x-1，最大值为1，最小值为-3，不满足要求，故B不正确；
C中函数y=sin(2x-
π
5
)-1，最大值为0，最小值为-2，不满足要求，故C不正确；
故选D．
点评：本题考查的知识点是由y=Asin（ωx+φ）的部分图象确定其解析式，其中排除法是解答选择题比较常用的方法，而根据函数的图象分析出函数的最值是解答本题的关键．
练习册系列答案
相关题目
已知幂函数y=f（x）的图象过点（2，
2
2
），试求出此函数的解析式，并作出图象，判断奇偶性、单调性．
已知函数f（x）=
1+alnxx
，（a∈R）．
（1）若函数f（x）在x=1处取得极值，求实数a的值；
（2）在（1）条件下，若直线y=kx与函数y=f（x）的图象相切，求实数k的值．
把函数y=lnx-2的图象按向量
α
=（-1，2）平移得到函数y=f（x）的图象．
（1）若x＞0，证明；f（x）＞
2x
x+2
；
（2不等式
1
2
x2≤f（x2）+m2-2bm-3对b∈[-1，1]，x∈[-1，1]时恒成立，求实数m的取值范围．
（文）设函数y=f（x）=x（x-a）（x-b）（a、b∈R）．
（Ⅰ）若a≠b，ab≠0，过两点（0，0）、（a，0）的中点作与x轴垂直的直线，此直线与函数y=f（x）的图象交于点P（x0，f（x0）），求证：函数y=f（x）在点P处的切 线过点（
4
3
3
，0）；
（Ⅱ）若a=b（a≠0），且当x∈[0，|a|+1]时f（x）＜2a2恒成立，求实数a的取值范围．
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示，给出关于f（x）的下列命题：
x -1 0 2 4 5
f（x） 1 2 0 2 1
①函数y=f（x）在x=2取到极小值；
②函数f（x）在[0，1]是减函数，在[1，2]是增函数；
③当1＜a＜2时，函数y=f（x）-a有4个零点；
④如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最小值为0．
其中所有正确命题是
①③④
①③④
（写出正确命题的序号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网