题目内容
（07年上海卷理）（12分）
体积为1的直三棱柱
中，
，
，求直线
与平面
所成角。
解析：法一： 由题意，可得体积
，
．连接
． 
，
平面
，
是直线
与平面所成的角．
，
，
则 
＝
．即直线与平面所成角的大小为．
法二： 由题意，可得
体积
，
，
如图，建立空间直角坐标系．
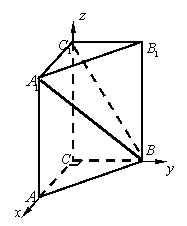
得点
，
，
． 则
，
平面的法向量为
．
设直线与平面所成的角为
，
与
的夹角为
，
则
， 
，
即直线与平面所成角的大小为
．
练习册系列答案
相关题目
为非零实数，则下列四个命题都成立：
②
③若
，则
，则
。则对于任意非零复数
。
中，
，
，求直线
与平面
所成角。 
的奇偶性 
是增函数，求实数
的范围
与半椭圆
组成的曲线称为“果圆”，其中
。如图，设点
，
，
是相应椭圆的焦点，
，
和
，
是“果圆” 与
，
轴的交点，
是边长为1的等边三角形，求“果圆”的方程；
，求
的取值范围；
，使得斜率为