题目内容
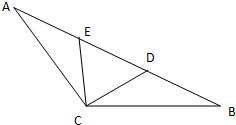 如图,在等腰三角形ABC中,∠ACB=120?,BC=AC=3,点D在线段AB上.
如图,在等腰三角形ABC中,∠ACB=120?,BC=AC=3,点D在线段AB上.(1)若CD=
| 3 |
(2)若点E在线段DA上,且∠DCE=30?,问:当∠DCB取何值时,△CDE的面积最小?并求出面积的最小值.
分析:(1)利用余弦定理,建立方程,即可求BD的长;
(2)由正弦定理,计算CD,CE,可得△CDE的面积,利用三角函数可求最值.
(2)由正弦定理,计算CD,CE,可得△CDE的面积,利用三角函数可求最值.
解答:解:(1)在△CDB中,∠CBD=30?,BC=3,CD=
,
由余弦定理,得CD2=BC2+BD2-2CB•BD•cos30°,…(2分)
即BD2-3
BD+6=0,解得,BD=
或2
.…(5分)
(2)设∠DCB=α,0°≤α≤90°,
在△CDB中,由正弦定理,得
=
,
即CD=
,
同理CE=
,…(8分)
所以,S△CDE=
CE•CD•sin30°=
=
=
=
…(12分)
∵0°≤α≤90°,∴0°≤2α≤180°.
∴当α=45°时,S△CDE的最小值为
=
.…(14分)
| 3 |
由余弦定理,得CD2=BC2+BD2-2CB•BD•cos30°,…(2分)
即BD2-3
| 3 |
| 3 |
| 3 |
(2)设∠DCB=α,0°≤α≤90°,
在△CDB中,由正弦定理,得
| CD |
| sin∠CBD |
| BC |
| sin∠CDB |
即CD=
| BC•sin30° |
| sin(150°-α) |
同理CE=
| BC•sin30° |
| sin(120°-α) |
所以,S△CDE=
| 1 |
| 2 |
| 9 |
| 16sin(150°-α)sin(120°-α) |
| 9 | ||
8
|
| 9 | ||
4
|
| 9 | ||
4
|
∵0°≤α≤90°,∴0°≤2α≤180°.
∴当α=45°时,S△CDE的最小值为
| 9 | ||
4(
|
9(2-
| ||
| 4 |
点评:本题考查余弦定理、正弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在等腰直角三角形ABC中,则AM<AC的概率为( )
如图,在等腰直角三角形ABC中,则AM<AC的概率为( ) (2013•徐州一模)如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且
(2013•徐州一模)如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且 .
.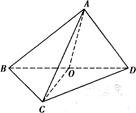
 时,求证:AO⊥平面BCD;
时,求证:AO⊥平面BCD; 的大小为
的大小为 时,求二面角
时,求二面角 的正切值.
的正切值. 如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且
如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且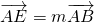 ,
,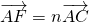 ,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则
,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则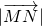 的最小值为________.
的最小值为________. 如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且
如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且 ,
, ,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则
,其中m,n∈(0,1).若EF,BC的中点分别为M,N,且m+4n=1,则 的最小值为 .
的最小值为 .