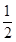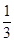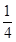题目内容
以下结论:①若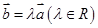 ,则
,则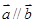 ;②若
;②若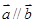 ,则存在实数
,则存在实数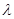 ,使
,使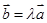 ;
;
③若 是非零向量,
是非零向量,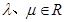 ,那么
,那么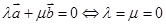 ;④平面内任意两个非零向量都可以作为表示平面内任意一个向量的一组基底。其中正确结论的个数是( )
;④平面内任意两个非零向量都可以作为表示平面内任意一个向量的一组基底。其中正确结论的个数是( )
A.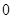 | B.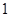 | C.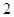 | D.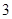 |
B
解析试题分析:①向量的数乘运算的几何意义知结论正确;②若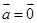 ,
,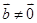 ,有
,有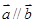 ,但不存在实数
,但不存在实数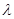 ,所以结论错;③
,所以结论错;③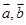 时相反向量,则
时相反向量,则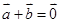 ,此时
,此时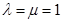 ,所以结论错; ④平面向量的基本定理,作为基底的两向量必须是不共线的非零向量,所以结论错.
,所以结论错; ④平面向量的基本定理,作为基底的两向量必须是不共线的非零向量,所以结论错.
考点: 1.平面向量的基本定理;2.向量的数乘运算.

练习册系列答案
相关题目
若向量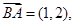
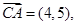 则
则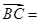 ( )
( )
A.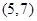 | B.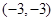 | C.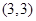 | D.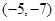 |
若平面向量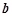 与
与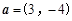 的夹角是
的夹角是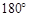 ,且
,且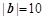 ,则
,则 ( ).
( ).
A.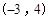 | B.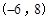 |
C.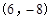 | D.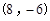 |
已知 ,
, 且
且 ∥
∥ ,则
,则 ( )
( )
| A.-3 | B. | C.0 | D. |
若三点P(1,1),A(2,-4),B(x,-14)共线,则( )
| A.x=-1 | B.x=3 | C.x=4 | D.x=51 |
设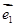 与
与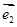 是不共线向量,
是不共线向量,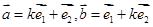 ,若
,若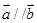 且
且 ,则实数
,则实数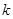 的值为( )
的值为( )
| A.0 | B.1 | C.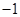 | D.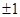 |
设x,y∈R,向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,则|a+b|= ( ).
A.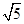 | B.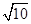 | C.2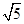 | D.10 |
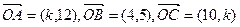 ,且A、B、C三点共线,则
,且A、B、C三点共线,则
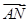 =λ
=λ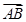 +μ
+μ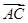 ,则λ+μ的值为( )
,则λ+μ的值为( )