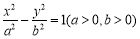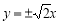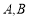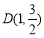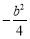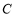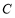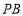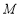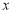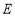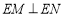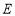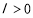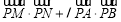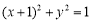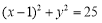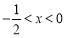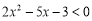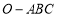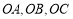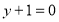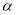题目内容
已知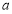 为实数,
为实数,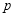 :点
:点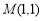 在圆
在圆 的内部;
的内部; 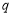 :
: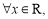 都有
都有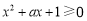 .
.
(1)若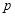 为真命题,求
为真命题,求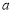 的取值范围;
的取值范围;
(2)若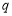 为假命题,求
为假命题,求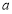 的取值范围;
的取值范围;
(3)若“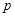 且
且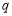 ”为假命题,且“
”为假命题,且“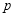 或
或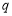 ”为真命题,求
”为真命题,求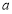 的取值范围.
的取值范围.
(1) 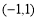 ;(2
;(2 )
)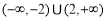 ;(3)
;(3) .
.
【解析】
试题分析:(1)关键在于根据点与圆的位置关系的结论得到不等式 ;
;
(2)关键在于由一元二次函数,一元二次不等式,一元二次方程的知识可知,若 都有
都有 ,则对应的二次函数开口向上,二次方程的判别式
,则对应的二次函数开口向上,二次方程的判别式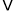 ≤0;
≤0;
(3)由简易逻辑知识可知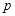 与
与 一真一假,然后利用集合的运算和解不等式组知识即可解决.
一真一假,然后利用集合的运算和解不等式组知识即可解决.
试题解析:(1)由题意得, ,解得
,解得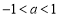 ,
,
故 为真命题时
为真命题时 的取值范围为
的取值范围为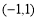 . 4分
. 4分
(2)若 为真命题,则
为真命题,则 ,解得
,解得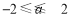 ,
,
故 为假命题时
为假命题时 的取值范围
的取值范围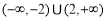 . 8分
. 8分
(3)由题意得,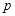 与
与 一真一假,从而
一真一假,从而
当 真
真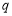 假时有
假时有 无解; 10分
无解; 10分
当 假
假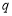 真时有
真时有 解得
解得 . 12分
. 12分
∴实数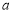 的取值范围是
的取值范围是 . 14分
. 14分
考点:(1) 点与圆的位置关系;(2)三个一元二次的关系;(3)简易逻辑;(4)集合的运算.

练习册系列答案
相关题目