题目内容
已知tan a=2,求| 2 |
| 3 |
| 1 |
| 4 |
分析:利用sin2α+cos2α=1的特点,把原式除以sin2α+cos2α,然后分子分母同时除以cos2α,转化成关于tanα的式子,最后把tanα的值代入即可求得答案.
解答:解:∵tana=2,
∴a的终边不落在坐标轴上
∴cosa≠0.
故原式=
=
=
=
.
∴a的终边不落在坐标轴上
∴cosa≠0.
故原式=
| ||||
| sin2a+cos2a |
=
| ||||
| tan2a+1 |
| ||||
| 4+1 |
| 11 |
| 60 |
点评:本题主要考查了同角三角函数基本关系的应用,三角函数恒等变换和化简求值,弦切互化问题.解题的过程巧妙的利用了sin2α+cos2α=1的特点,完成有由弦到切的转化.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
(三角求值)已知tan(α+
)=2,则cos2α=( )
| π |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
 的值.
的值.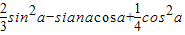 的值.
的值.