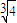题目内容
如果在区间[1,2]上函数f(x)=x2+px+q与g(x)=x+ 在同一点取相同的最小值,那么f(x)在该区间上的最大值是
在同一点取相同的最小值,那么f(x)在该区间上的最大值是
- A.4+

 +
+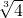
- B.4-

 +
+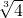
- C.1-

 +
+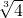
- D.以上答案都不对
B
分析:在区间[1,2]上函数g(x)=x+ ≥3
≥3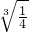 ,当且仅当x=
,当且仅当x= 时,取等号.故在区间[1,2]上函数f(x)=x2+px+q在x=
时,取等号.故在区间[1,2]上函数f(x)=x2+px+q在x= 时对最小值3
时对最小值3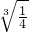 ,由此能求出x=2时,f(x)在该区间上的最大值.
,由此能求出x=2时,f(x)在该区间上的最大值.
解答:在区间[1,2]上函数g(x)=x+
=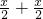 +
+ ≥3
≥3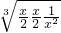 =3
=3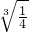 ,
,
当且仅当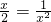 ,即x=
,即x= 时,取等号.
时,取等号.
∴在区间[1,2]上函数f(x)=x2+px+q在x= 时对最小值3
时对最小值3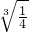 ,
,
∴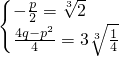 ,
,
解得p=-2 ,q=3
,q=3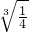 +
+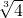 .
.
∴x=2时,f(x)在该区间上的最大值=4-4 +3
+3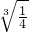 +
+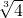 =4-
=4-
 +
+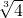 .
.
故选B.
点评:本题考查利用导数求闭区间上函数最值的应用,解题时要认真审题,仔细解答,注意均值定理的合理运用.
分析:在区间[1,2]上函数g(x)=x+
 ≥3
≥3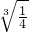 ,当且仅当x=
,当且仅当x= 时,取等号.故在区间[1,2]上函数f(x)=x2+px+q在x=
时,取等号.故在区间[1,2]上函数f(x)=x2+px+q在x= 时对最小值3
时对最小值3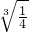 ,由此能求出x=2时,f(x)在该区间上的最大值.
,由此能求出x=2时,f(x)在该区间上的最大值.解答:在区间[1,2]上函数g(x)=x+

=
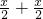 +
+ ≥3
≥3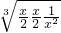 =3
=3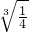 ,
,当且仅当
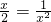 ,即x=
,即x= 时,取等号.
时,取等号.∴在区间[1,2]上函数f(x)=x2+px+q在x=
 时对最小值3
时对最小值3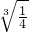 ,
,∴
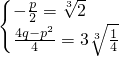 ,
,解得p=-2
 ,q=3
,q=3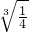 +
+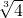 .
.∴x=2时,f(x)在该区间上的最大值=4-4
 +3
+3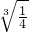 +
+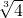 =4-
=4-
 +
+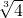 .
.故选B.
点评:本题考查利用导数求闭区间上函数最值的应用,解题时要认真审题,仔细解答,注意均值定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
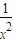 在同一点取相同的最小值,那么f(x)在该区间上的最大值是( )
在同一点取相同的最小值,那么f(x)在该区间上的最大值是( )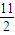
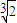 +
+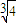

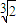 +
+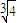

 +
+