题目内容
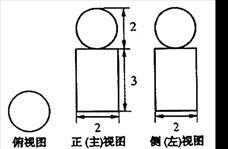
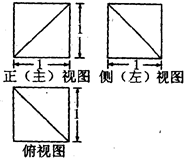
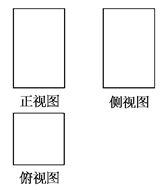
已知三棱锥 的三视图如图所示.
的三视图如图所示.

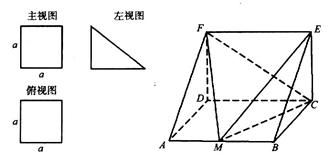
(Ⅰ)求证: 是直角三角形;
是直角三角形;
 求三棱锥
求三棱锥 是全面积;
是全面积;
(Ⅲ)当点 在线段
在线段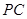 上何处时,
上何处时, 与平面
与平面 所成的角为
所成的角为 .
.
 的三视图如图所示.
的三视图如图所示.
(Ⅰ)求证:
 是直角三角形;
是直角三角形; 求三棱锥
求三棱锥 是全面积;
是全面积;(Ⅲ)当点
 在线段
在线段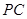 上何处时,
上何处时, 与平面
与平面 所成的角为
所成的角为 .
.1)根据视图中所给的数据特证可以证明BC⊥面PAB,由线面垂直的性质证出BC⊥PB,由此证得三角形为直角三角形,(2)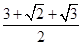
(3)当 为线段
为线段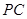 的中点时,
的中点时, 与平面
与平面 所成的角为
所成的角为
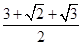
(3)当
 为线段
为线段 的中点时,
的中点时, 与平面
与平面 所成的角为
所成的角为
试题分析:解析:(Ⅰ)由三视图可得:
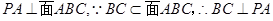
由俯视图知
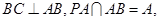
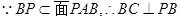
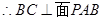 ,
,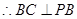
故
 是以
是以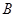 为直角顶点的直角三角形. 4分
为直角顶点的直角三角形. 4分(Ⅱ)
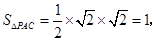 且
且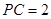
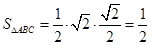 ,
,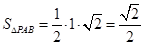 ,且
,且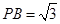
由(Ⅰ)知
 是直角三角形,故其面积为
是直角三角形,故其面积为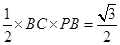
故三棱锥
 的全面积为
的全面积为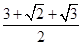 8分
8分(Ⅲ)在面
 内过
内过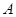 做
做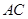 的垂线
的垂线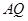 ,
,以
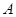 为原点,
为原点, 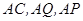 所在直线分别为
所在直线分别为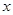 轴、
轴、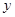 轴 、
轴 、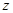 轴建立空间直角坐标系,如图所示
轴建立空间直角坐标系,如图所示则
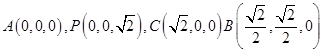
设
 为面
为面 的一个法向量,
的一个法向量,
则

 取
取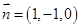
设
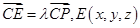 ,
,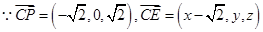 ,
,
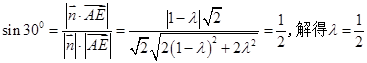
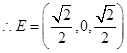 ,故当
,故当 为线段
为线段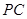 的中点时,
的中点时, 与平面
与平面 所成的角为
所成的角为 ……13分
……13分点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是四棱锥的体积,其公式为
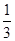 ×底面积×高.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”,三视图是新课标的新增内容,在以后的高考中有加强的可能.用向量法求线面角是空间向量的一个重要运用,其步骤是:一、建立坐标系,表示出相应量的坐标,二、求出直线的方向向量以及面的法向量,三、利用公式表示线面角或者面面角的三角函数值求角.用向量解决几何问题是新课标的新增内容,这几年高考中此工具是一个常考常新的类型.
×底面积×高.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”,三视图是新课标的新增内容,在以后的高考中有加强的可能.用向量法求线面角是空间向量的一个重要运用,其步骤是:一、建立坐标系,表示出相应量的坐标,二、求出直线的方向向量以及面的法向量,三、利用公式表示线面角或者面面角的三角函数值求角.用向量解决几何问题是新课标的新增内容,这几年高考中此工具是一个常考常新的类型.
练习册系列答案
相关题目











 π
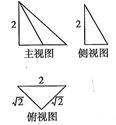
π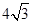 ,则这个圆锥的全面积是( )
,则这个圆锥的全面积是( )

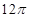

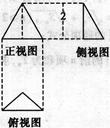
 ,则该三棱柱的侧棱长( ).
,则该三棱柱的侧棱长( ).


