题目内容
9.椭圆$\frac{x^2}{4}+{y^2}=1$两个焦点分别是F1,F2,点P是椭圆上任意一点,则$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的取值范围是[-2,1].分析 求出椭圆的焦点坐标,设P的坐标,利用向量的数量积化简,通过椭圆的范围,求解即可.
解答 解:椭圆$\frac{x^2}{4}+{y^2}=1$两个焦点分别是${F_1}(-\sqrt{3},0),{F_2}(\sqrt{3},0)$,
设P(x,y),则$\overrightarrow{P{F_1}}=(-\sqrt{3}-x,-y)$,$\overrightarrow{P{F_2}}=(\sqrt{3}-x,-y)$,$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=(-\sqrt{3}-x)(\sqrt{3}-x)+{y^2}={x^2}+{y^2}-3$,
因为${y^2}=1-\frac{x^2}{4}$,
代入可得$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=\frac{3}{4}{x^2}-2$,而-2≤x≤2,$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的取值范围是[-2,1]
故答案为:[-2,1].
点评 本题考查椭圆的几何性质,向量的数量积的应用,考查计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.已知lg2=0.3010,由此可以推断22015是( )位整数.
| A. | 605 | B. | 606 | C. | 607 | D. | 608 |
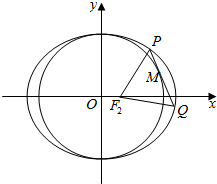 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点($\frac{3\sqrt{2}}{2}$,2)在椭圆上.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点($\frac{3\sqrt{2}}{2}$,2)在椭圆上.