Question

【题目】以下命题：
①若x≠1或y≠2，则x+y≠3；
②若空间向量 ， 与空间中任一向量都不能组成空间的一组基底，则 与 共线；
③命题“x∈R，使得x2+x+1＜0”的否定是：“x∈R，均有x2+x+1＜0”；
④若A、B为两个定点，K为正常数，若|PA|+|PB|=K，则动点P的轨迹是椭圆；
⑤已知抛物线y2=2px，以过焦点的一条弦AB为直径作圆，则此圆与准线相切．
其中真命题有（ ）个．
A.1
B.2
C.3
D.4

Answer 1

【答案】B
【解析】解：①若x≠1或y≠2，则x+y≠3得逆否命题为若x+y=3，则x=1且y=2，当x=3，y=0时，x=1且y=2不成立，即逆否命题为假命题，则原命题为假命题；故①错误，
②若空间向量 与空间中任一向量都不能组成空间的一组基底，则 与 共线，故②正确；
③命题“x∈R，使得x2+x+1＜0”的否定是：“x∈R，均有x2+x+1≤0”；故③错误，
④，若A、B为两个定点，K为正常数，若|PA|+|PB|=K＞|AB|，则动点P的轨迹是椭圆，
若|PA|+|PB|=K=|AB|，则动点P的轨迹是线段，故④错误；
⑤取AB的中点M，分别过A、B、M作准线的垂线AP、BQ、MN，垂足分别为P、Q、N，如图所示：
由抛物线的定义可知，|AP|=|AF|，|BQ|=|BF|，
在直角梯形APQB中，|MN|= （|AP|+|BQ|）= （|AF|+|BF|）= |AB|，
故圆心M到准线的距离等于半径，
∴以AB为直径的圆与抛物线的准线相切，故⑤正确；
故真命题为：②⑤，
故选：B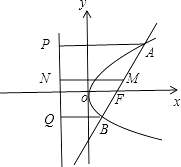

【考点精析】关于本题考查的命题的真假判断与应用，需要了解两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能得出正确答案．