题目内容
下列命题中,真命题是( )A.?x∈R,x2-x-1>0
B.?α,β∈R,sin(α+β)<sinα+sinβ
C.函数y=2sin(x+
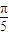 )的图象的一条对称轴是x=
)的图象的一条对称轴是x=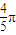
D.?α,β∈R,sin(α+β)=cosα+cosβ
【答案】分析:对于全称命题A,B,欲说明其为假,只须举一个反例即可;对于选项C,只须将x的值代入,看函数是否取最值即可,能取到最值就是函数的对称轴;对于存在性命题D,欲说明其为假,也只须找一个特例即可.
解答:解:A:∵x2-x-1=(x- )2-
)2- >-
>- 恒成立,当x=
恒成立,当x= 时,x2-x-1>0不成立,故?x∈R,x2-x-1>0是假命题.
时,x2-x-1>0不成立,故?x∈R,x2-x-1>0是假命题.
B:当α=0,β=0时,sin(α+β)=0,sinα+sinβ=0,sin(α+β)<sinα+sinβ不成立,故B为假;
C:当x=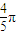 时,y=2sin(x+
时,y=2sin(x+ )=2sin(
)=2sin(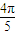 +
+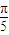 )=0,不取最值,故直线x=
)=0,不取最值,故直线x=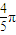 不是f(x)的对称轴;
不是f(x)的对称轴;
D:∵sin(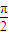 +
+ )=cos
)=cos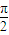 +cos
+cos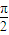 =0,
=0,
∴?α,β∈R,使sin(α+β)=cosα+cosβ成立.D为真;
故选D.
点评:本题考查的知识点是命题的真假,特称命题,全称命题,属于基础题.
解答:解:A:∵x2-x-1=(x-
 )2-
)2- >-
>- 恒成立,当x=
恒成立,当x= 时,x2-x-1>0不成立,故?x∈R,x2-x-1>0是假命题.
时,x2-x-1>0不成立,故?x∈R,x2-x-1>0是假命题.B:当α=0,β=0时,sin(α+β)=0,sinα+sinβ=0,sin(α+β)<sinα+sinβ不成立,故B为假;
C:当x=
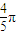 时,y=2sin(x+
时,y=2sin(x+ )=2sin(
)=2sin(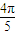 +
+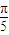 )=0,不取最值,故直线x=
)=0,不取最值,故直线x=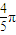 不是f(x)的对称轴;
不是f(x)的对称轴;D:∵sin(
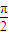 +
+ )=cos
)=cos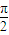 +cos
+cos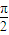 =0,
=0,∴?α,β∈R,使sin(α+β)=cosα+cosβ成立.D为真;
故选D.
点评:本题考查的知识点是命题的真假,特称命题,全称命题,属于基础题.

练习册系列答案
相关题目
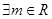 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1