题目内容
已知函数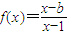 ,它的图象过点(2,-1).
,它的图象过点(2,-1).(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式:
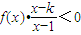 、
、
【答案】分析:(1)把点的坐标代入函数解析式求出待定系数,从而得到函数解析式.
(2)将不等式进行等价转化为一元二次不等式组,分类讨论解得情况,最后把各种情况得到的解集取并集.
解答:解:(1)依题意函数f(x)过点(2,-1),有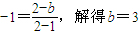 .
.
故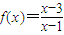 .(4分)
.(4分)
(2)由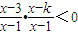 ,得
,得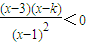 .
.
原不等式等价于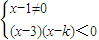 (6分)
(6分)
当k>3时,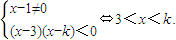 (8分)
(8分)
当1<k<3时,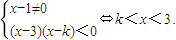 (10分)
(10分)
当k=3时,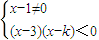
此时不等式组无解(12分)
所以,当k>3时,不等式的解集为{x|3<x<k};
当1<k<3时,不等式的解集为{x|k<x<3};
当k=3时,不等式的解集为空集.(13分)
点评:本题考查用待定系数法求函数解析式,把分式不等式进行进行等价转化为一元二次不等式组来解,体现等价转化和分类讨论的数学思想.
(2)将不等式进行等价转化为一元二次不等式组,分类讨论解得情况,最后把各种情况得到的解集取并集.
解答:解:(1)依题意函数f(x)过点(2,-1),有
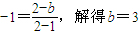 .
.故
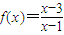 .(4分)
.(4分)(2)由
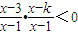 ,得
,得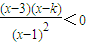 .
.原不等式等价于
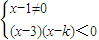 (6分)
(6分)当k>3时,
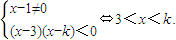 (8分)
(8分)当1<k<3时,
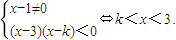 (10分)
(10分)当k=3时,
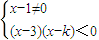
此时不等式组无解(12分)
所以,当k>3时,不等式的解集为{x|3<x<k};
当1<k<3时,不等式的解集为{x|k<x<3};
当k=3时,不等式的解集为空集.(13分)
点评:本题考查用待定系数法求函数解析式,把分式不等式进行进行等价转化为一元二次不等式组来解,体现等价转化和分类讨论的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
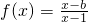 ,它的图象过点(2,-1).
,它的图象过点(2,-1).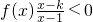 、
、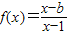 ,它的图象过点(2,-1).
,它的图象过点(2,-1).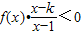 、
、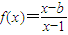 ,它的图象过点(2,-1).
,它的图象过点(2,-1).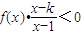 、
、