题目内容
已知f(x)=lg(x+1),g(x)=2lg(2x+t),(t∈R是参数).
(1)当t=–1时,解不等式f(x)≤g(x);
(2)如果x∈[0,1]时,f(x)≤g(x)恒成立,求参数t的取值范围.
(1)原不等式的解集为{x|x≥![]() }(2)t的取值范围是t≥1
}(2)t的取值范围是t≥1
解析:
(1)原不等式等价于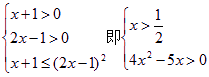
即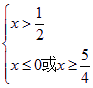 ∴x≥
∴x≥![]()
∴原不等式的解集为{x|x≥![]() }.
}.
(2)x∈[0,1]时,f(x)≤g(x)恒成立.
∴x∈[0,1]时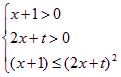 恒成立
恒成立![]() 即
即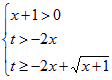 恒成立即x∈[0,1]时,t≥–2x+
恒成立即x∈[0,1]时,t≥–2x+![]() 恒成立,
恒成立,
于是转化为求–2x+![]() ,x∈[0,1]的最大值问题
,x∈[0,1]的最大值问题
令μ=![]() ,则x=μ2–1,则μ∈[1,
,则x=μ2–1,则μ∈[1,![]() ].
].
∴2x+![]() =–2(μ–
=–2(μ–![]() )2+
)2+![]() .
.
当μ=1即x=0时,–2x+![]() 有最大值1
有最大值1
∴t的取值范围是t≥1.

练习册系列答案
相关题目
已知f(x)=lg(
-1)的图象关于( )对称.
| 2 |
| 1-x |
| A、y轴 | B、x轴 |
| C、原点 | D、直线y=x |