题目内容
已知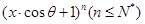 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含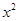 的系数与
的系数与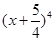 的展开式中
的展开式中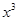 的系数相等,则锐角
的系数相等,则锐角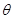 的值是
的值是
A. | B. | C. | D.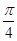 |
D
解析考点:二项式定理的应用;排列、组合的实际应用.
分析:由题意,(x?cosθ+1)n的展开式中二项式系数之和为32,即2n=32,可得n=5;由二项式定理求得(x?cosθ+1)n展开式中x2项的系数与(x+  )4的展开式中x3的系数,令两者相等根据题意,可得10cos2θ=5,解可得cos2θ=
)4的展开式中x3的系数,令两者相等根据题意,可得10cos2θ=5,解可得cos2θ= 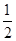 ,又由θ为锐角,可得cosθ的值,进而可得答案.
,又由θ为锐角,可得cosθ的值,进而可得答案.
解:由(x?cosθ+1)n(n≤N*)的展开式中二项式系数之和为32,得2n=32,则n=5;
故(x?cosθ+1)n(n≤N*)展开式中x2的系数为C53cos2θ=10cos2θ,
(x+ )4的展开式中x3的系数为
)4的展开式中x3的系数为 ?
? =5,
=5,
根据题意,有10cos2θ=5,则cos2θ=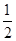 ,
,
又由θ为锐角,则cosθ=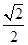 ,
,
即θ=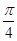 ;
;
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
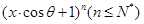 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含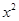 的系数与
的系数与 的展开式中
的展开式中 的系数相等,则锐角
的系数相等,则锐角 的值是
的值是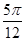 B.
B.
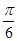 C.
C.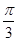 D.
D. 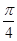
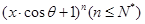 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含 的系数与
的系数与 的展开式中
的展开式中 的系数相等,则锐角
的系数相等,则锐角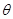 的值是( )
的值是( ) B.
B.
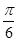 C.
C.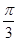 D.
D. 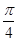
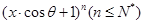 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含 的系数与
的系数与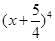 的展开式中
的展开式中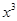 的系数相等,则锐角
的系数相等,则锐角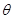 的值是
的值是 B.
B.
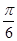 C.
C. D.
D. 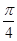
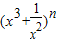 的展开式中,所有二项式系数的和为32,其展开式中的常数项为 (用数字答).
的展开式中,所有二项式系数的和为32,其展开式中的常数项为 (用数字答).