题目内容
设直线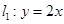 与直线
与直线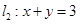 交于
交于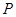 点.
点.
(1)当直线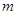 过
过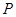 点,且与直线
点,且与直线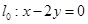 垂直时,求直线
垂直时,求直线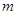 的方程;
的方程;
(2)当直线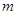 过
过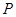 点,且坐标原点
点,且坐标原点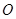 到直线
到直线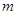 的距离为
的距离为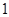 时,求直线
时,求直线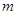 的方程.
的方程.
【答案】
(1) (2)
(2) 或
或 .
.
【解析】
试题分析:解:由 ,解得点
,解得点 . 2分
. 2分
(1)因为 ⊥
⊥ ,所以直线
,所以直线 的斜率
的斜率 , 4分
, 4分
又直线 过点
过点 ,故直线
,故直线 的方程为:
的方程为: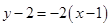 ,
,
即 . 6分
. 6分
(2)因为直线 过点
过点 ,当直线
,当直线 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为 ,即
,即 . 7分
. 7分
所以坐标原点 到直线
到直线 的距离
的距离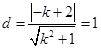 ,解得
,解得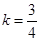 , 9分
, 9分
因此直线 的方程为:
的方程为: ,即
,即 . 10分
. 10分
当直线 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为 ,验证可知符合题意. 13分
,验证可知符合题意. 13分
综上所述,所求直线 的方程为
的方程为 或
或 . 14分
. 14分
考点:两直线的位置关系的运用
点评:解决求解直线的关键是找到点和斜率,一般易错点就是忽略对于斜率是否存在的讨论,属于基础题。

练习册系列答案
相关题目
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为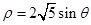 。
。 。若点
。若点 的坐标为(3,
的坐标为(3, ),求
),求 。
。 与直线
与直线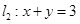 交于
交于 点.
点. 过
过 垂直时,求直线
垂直时,求直线 到直线
到直线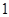 时,求直线
时,求直线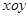 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).在极坐标系(与直角坐标系
为参数).在极坐标系(与直角坐标系 为极点,以
为极点,以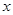 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆 的方程为
的方程为 .
. 、
、 ,若点
,若点 的坐标为
的坐标为 ,求
,求 的值.
的值.