题目内容
如果点P在平面区域 上,
上,
点Q在曲线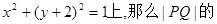 最小值为
最小值为
 上,
上,点Q在曲线
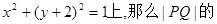 最小值为
最小值为A.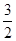 | B.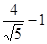 | C.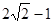 | D.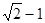 |
A
分析:作出可行域,将|PQ|的最小值转化为圆心到可行域的最小值,结合图形,求出|CP|的最小值,减去半径得PQ|的最小值.
解答:解:作出可行域,要使PQ|的最小,
只要圆心C(0,-2)到P的距离最小,
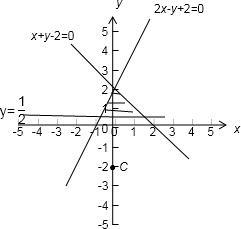
结合图形当P(0,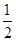 )时,CP最小为
)时,CP最小为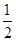 +2=
+2=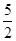
又因为圆的半径为1
故PQ|的最小为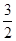 故选A
故选A
解答:解:作出可行域,要使PQ|的最小,
只要圆心C(0,-2)到P的距离最小,

结合图形当P(0,
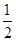 )时,CP最小为
)时,CP最小为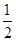 +2=
+2=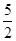
又因为圆的半径为1
故PQ|的最小为
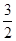 故选A
故选A
练习册系列答案
相关题目
 下,目标函数
下,目标函数 的最小值是.
的最小值是.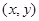 位于线性约束条件
位于线性约束条件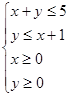 所表示的区域内(含边界),则目标函数
所表示的区域内(含边界),则目标函数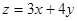 的最大值是
的最大值是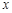 、
、 满足约束条件:
满足约束条件: ,则
,则 的最大值是( )
的最大值是( )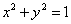 上一点,Q是满足
上一点,Q是满足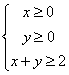 的平面区域内的点,则|PQ|的最小值为( )
的平面区域内的点,则|PQ|的最小值为( )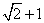
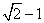
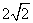
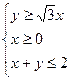 ,在可行域内任取一点
,在可行域内任取一点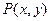 ,则点
,则点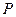 满足
满足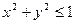 的概率是 .
的概率是 .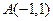 ,
, 是坐标原点,点
是坐标原点,点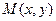 的坐标满足
的坐标满足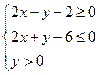 则
则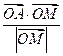 的取值范围是________。
的取值范围是________。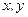 满足
满足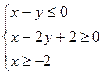 ,则
,则 的最小值是_ _.
的最小值是_ _. 、
、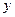 满足约束条件
满足约束条件 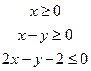 , 则
, 则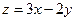 的最大值为 ( )
的最大值为 ( )